Предмет: Алгебра,
автор: an4erl2n
Решить систему уравнений:
Приложения:
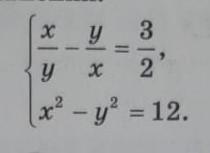
an4erl2n:
если вам лень полностью все расписывать, просто подскажите что тут надо подставить
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: ХацукиМилори
Предмет: Русский язык,
автор: 125436789hi
Предмет: Русский язык,
автор: Swy
Предмет: Алгебра,
автор: Renatata1
Предмет: Алгебра,
автор: Anchik1441