Предмет: Математика,
автор: Аноним
Помогите, пожалуйста!
Исследовать числовой ряд на сходимость.
Приложения:
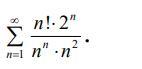
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Окружающий мир,
автор: 5364536564545
Предмет: Русский язык,
автор: Girl050302
Предмет: Русский язык,
автор: tasokolenko
Предмет: Қазақ тiлi,
автор: unknown2015
Предмет: Литература,
автор: Lesay89