Question

Помогите, пожалуйста :)
В цилиндре через две образующие проведено сечение, площадь которого относится к площади осевого сечения как 1:√5. Найдите расстояние от оси цилиндра до плоскости сечения, если осевое сечение сечение цилиндра - квадрат, площадь которого 45 см^2.

Answer 1

Ответ:

ОЕ = 3

Объяснение:

Дано:. Цилиндр-ORh,

Где: О-центр основания;

R- радиус; h- высота цил-ра.

Sосев=45; Scеч : Sосев = 1 : √5

ОЕ =? ( Расстояние от О до Sсеч)

В осевом сечении квадрат Sосев=45;

Sосев=2Rh. =>. 2R=h=√45=3√5,

R=1,5√5;. h=3√5

Sсеч=h*AB (AB-хорда).

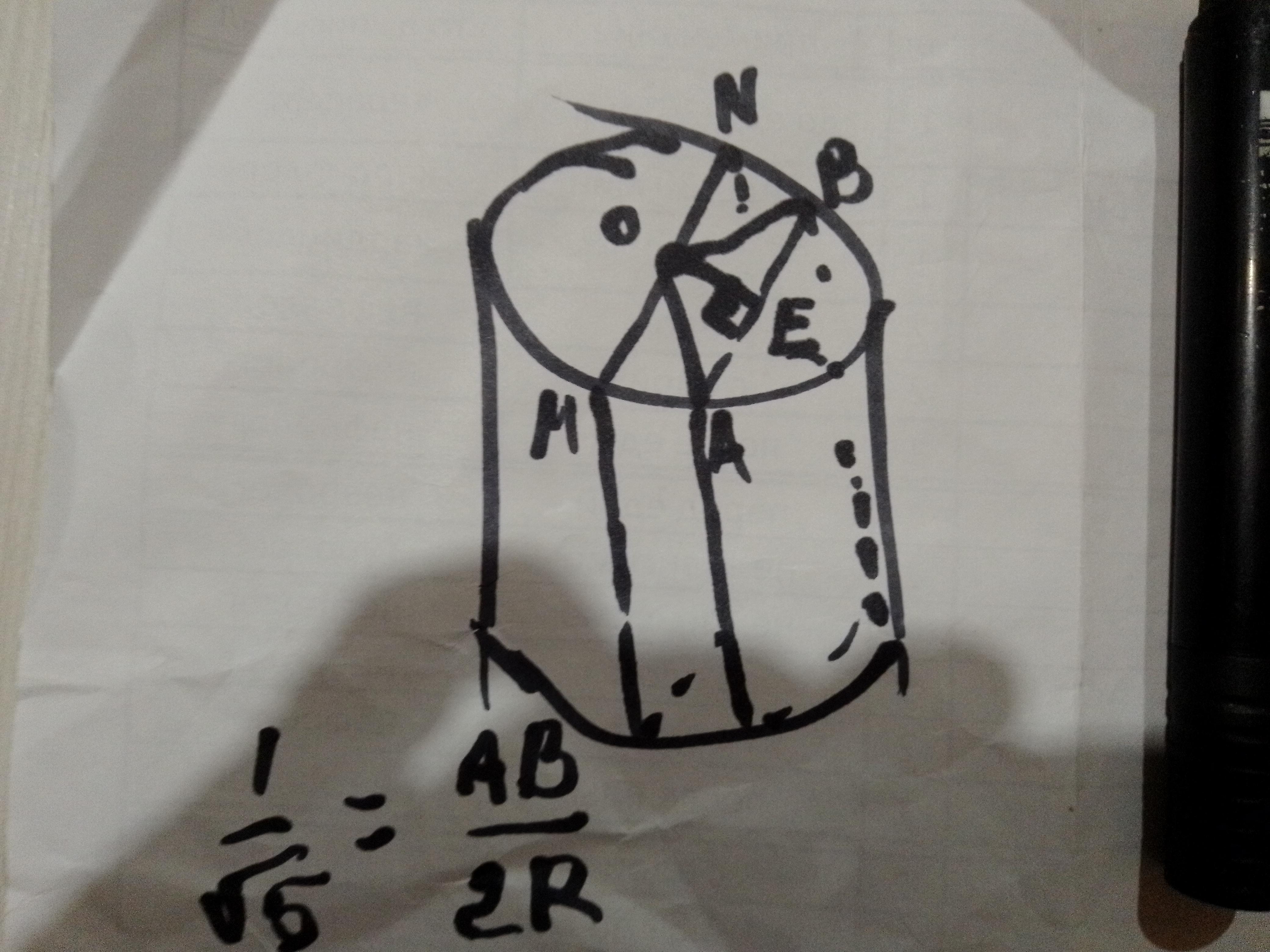
Sсеч : Sосев = 1 :√5 = AB*h : 2R*h; из пропорции выражается АВ

АВ = 2R/√5= 3√5/√5=3

Далее рассматриваем прямоугольный ∆АЕО в основании , где О-центр; АО=R,,. <E=90;

AE=1/2 AB ( из равнобедренного ∆ АОВ, где О-центр, ОА=ОВ=R )

ОЕ - искомая величина,

ОЕ= √(R^2-[AE]^2)

AE=1,5;. R=1,5√5

OE = √( [1,5√5]^2-1,5^2) если 1,5^2 как общий множитель вынести за скобки, а вдальнейшем и за знак корня, выражение примет вид

ОЕ = 1,5√ ([√5]^2-1 ) = 1,5√4 = 3