Question

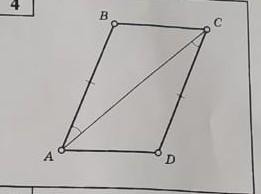
ABCD - четырехугольник. BA = CD. угол BAC = углу ACD. Докажите что ABCD - параллелограмм. ПОМОГИТЕ ПОЖАЛУЙСТА!​

Answer 1

Відповідь:

Пояснення:

В данном четырехугольнике проведена диагональ АС, которая делит его на два треугольника - АВС и ADC. Поскольку угла ВАС и ACD равные и стороны CD и АВ равные по условию, а сторона АС является общей, то по первому признаку равенства треугольников - они равны. Собственно и ВС=AD, а также АВС = ADC.

Поскольку противолежащие стороны у четырехугольника равны, а также равны противолежащие углы, и диагональю четырехугольник разделен на два равных треугольника, то это нам дает право сделать вывод, что данный четырехугольник является параллелограммом.