В ромбе одна из диагоналей равна стороне. Найдите углы ромба.
Ответы
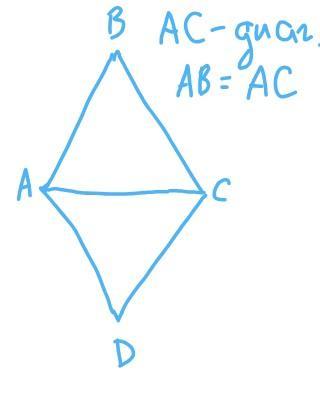
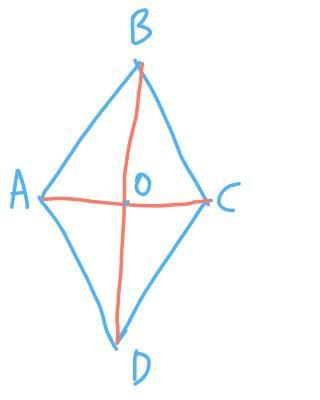
Пусть ABCD — ромб,
AC и BD — диагонали ромба, пересекаются в точке O,
AB = AC.
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам (свойство ромба) => угол AOB = 90°, AO = OC = 1/2 × AC,
AC = 2 × AO = AB, AO = 1/2 × AB.
Рассмотрим треугольник AOB, он прямоугольный (угол AOB = 90°), AB — гипотенуза (лежит напротив угла в 90°), AO и BO — катеты. Катет AO равен половине гипотенузы AB. По признаку прямоугольного треугольника, если один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° => угол ABO = 30°. Сумма углов треугольника равна 180° => угол BAO = 180° - 30° - 90° = 60°.
Диагонали ромба являются биссектриссами его углов (свойство ромба) => угол A = 2 × угол BAO = 2 × 60° = 120°, угол B = 2 × угол ABO = 2 × 30° = 60°.
Противоположные углы ромба равны (свойство ромба) => угол A = угол C = 120°, угол B = угол D = 60°.
Ответ: A = 120°, B = 60°, C = 120°, D = 60°.