Question

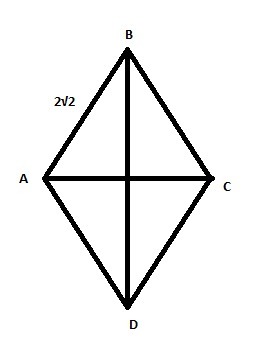
Площадь ромба равна 4 корня из 2, а его сторона 2 корня из двух. Найдите углы ромба.

Answer 1

$S=4sqrt{2}\AB=BC=CD=DA=2sqrt{2}$

∠A,B,C,D - ?

Находить углы мы будем из формулы площади для ромба $S=a^2 sinalpha$ , где α - острый угол.

Так как у нас есть и площадь и сторона найдём острый угол:

$S=a^2 * sinABC\\ 4sqrt{2}=(2sqrt{2})^2*sinABC\\ 4sqrt{2}=4*2*sinABC\\ 4sqrt{2} =8sinABC\\ 8sinABC=4sqrt{2} mid div 8\\sinABC=frac{sqrt{2} }{2}$

Отсюда сам ∠ABC = 45° ( из таблицы синусов/косинусов)

Так как это ромб, противоположные углы равны, значит ∠ABC=∠ADC=45°.

Найдём тупые углы ∠BAD=∠BCD. Обозначим их за x° .

Так как сумма всех углов ромба = 360°:

x°+x°+45°+45°=360°

2x°=360°-90°

2x°=270°

x=135°

Тупые углы по 135°.

Ответ: ∠A=135° , ∠B=45° , ∠C=135° , ∠D=45 ° .