Предмет: Геометрия,
автор: daariiyaacherginetss
У ромбi ABCD: CD=3см, АС=9см, DB=8см. <<С=80º.0-точка перетину діагоналей ромба. Знайдіть периметр трикутника АОВ та його кути. СРОЧНО ПОМОГИТЕ!!
Ответы
Автор ответа:
0
Ответ:
см
∠AOB=90°
∠ABO=50°
∠BAO=40°
Объяснение:
Дано: ABCD - ромб
CD = 3 см
AC = 9 см
BD = 8 см
∠C = 80°
Найти: PΔ = ?
∠AOB=?
∠ABO=?
∠BAO=?
Решение: т.к ABCD - ромб, то у него все стороны равны ⇒ CD=BC=AB=AD=3 см
Диагонали ромба точкой пересечения делятся пополам: BO=OD=8/2=4 см; AO=OC=9/2=4,5 см
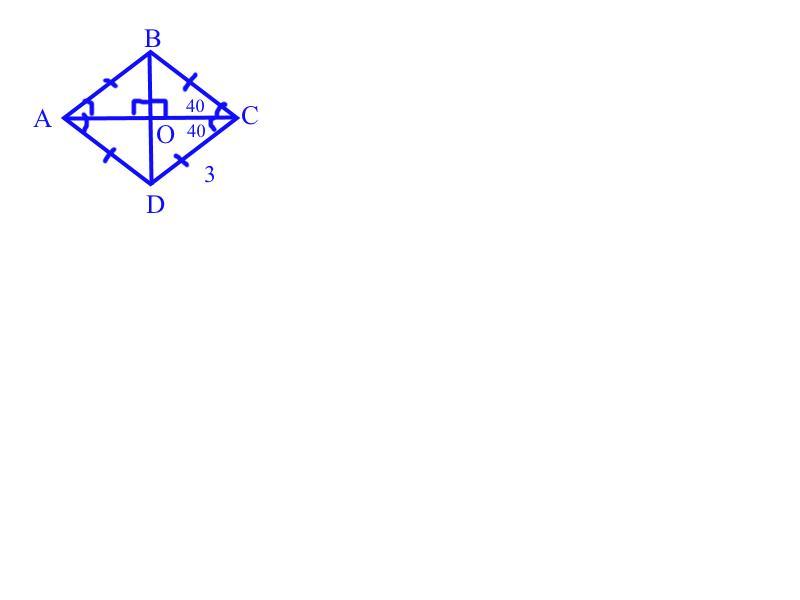
Противолежащие углы ромба равны ⇒ ∠C=∠A=80°, но т.к диагонали ромба являются биссектрисами его углов, то ∠OAD=∠BAO=80/2=40°
Диагонали ромба пересекаются под прямым углом ⇒ ∠AOB=90°
В ΔABO - прямоугольном, найдем ∠ABO. Сумма острых углов в прямоугольном треугольнике = 90°
∠ABO+∠BAO=90; ∠ABO=90-∠BAO; ∠ABO=90-40; ∠ABO=50°
Периметр - сумма длин всех сторон, тогда см
Приложения:
Похожие вопросы
Предмет: Технология,
автор: Ксенечка01
Предмет: Английский язык,
автор: 11вопрос1
Предмет: Русский язык,
автор: анеля232
Предмет: ОБЖ,
автор: Alina522542