Предмет: Алгебра,
автор: dfsgvss
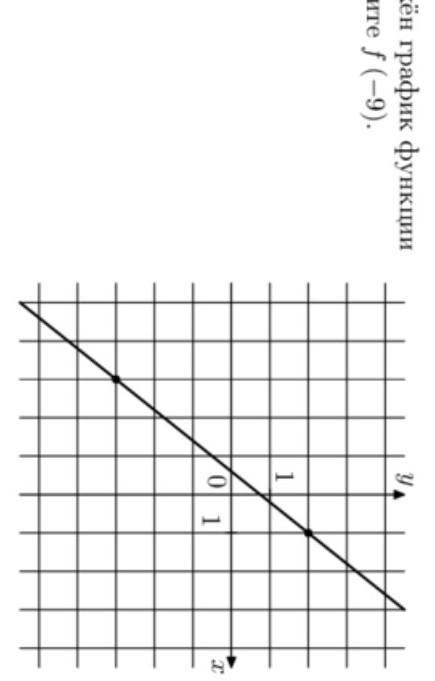
на рисунке изображен график функции f(x)=kx+b. найдите f(-9)
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
На рисунке изображен график функции
Найти : .
Рассмотрим рисунок. На рисунке изображена прямая, которая проходит через точки (1; 2) и (-3; -3) .
Подставим координаты данных точек в заданное уравнение, составим систему и найдем значения k и b.
Тогда функция принимает вид:
Найдем значение функции при х= - 9. Для этого подставим вместо х заданное значение -9.
#SPJ3
Похожие вопросы
Предмет: Українська мова,
автор: КириллОгольцов
Предмет: Русский язык,
автор: лапакота
Предмет: Английский язык,
автор: alena011099
Предмет: Английский язык,
автор: arakelyan73