Предмет: Алгебра,
автор: gohajjfe
решите уровнение
(x+y)³ (x-y)²=27
(x-y)³ (x+y)²=9
Приложения:
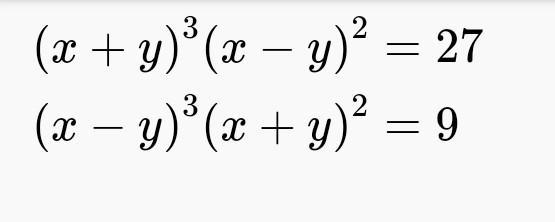
Ответы
Автор ответа:
1
Ответ:
Объяснение:
⇔
⇔
⇔
⇔
1) Поделим уравнения друг на друга:
=
= 3
3(x-y)=x+y
3x-3y=x+y
3x-x-3y-y=0
2x-4y=0 / 2
x-2y = 0
x = 2y
2)Решим (2y-y)³(2y+y)² = 9
y³ * (3y)² = 9
y³ * 9y² = 9 /9
y³ * y² = 1
= 1
y=1
Похожие вопросы
Предмет: Русский язык,
автор: katerinabebkina
Предмет: Английский язык,
автор: adelyar75
Предмет: Русский язык,
автор: aselzhubataeva
Предмет: Математика,
автор: shepilovahanna
Предмет: Математика,
автор: shalash27282930