Question

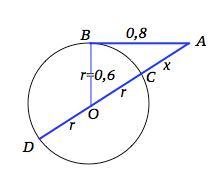
Через точку А провели секущую AD,проходящую через центр окружности О, и касательную АВ.Найти AD, если АВ=0,8дм, а радиус окружности 0,6 дм​

Answer 1

Ответ: 1,6 см

Объяснение:

  Рассмотрим 2 варианта решения ( в зависимости от изучаемой темы).

1) Квадрат касательной равен произведению секущей на ее внешнюю часть.

Пусть С – вторая точка пересечения секущей и окружности. АС - внешняя часть секущей. Примем АС=х. Тогда AD=2r+x=1,2+x

АВ²=AD•AC

0,64=(1,2x+x)•x⇒

x²+1,2x-64=0

Решив уравнение, получим х₁=0,4, х₂= -1,6 ( отрицательная величина не может быть длиной отрезка).

AD=1,2+0,4=1,6 (см).

2) ВО - радиус, проведенный в точку касания ⇒ ВО⊥АВ. Из прямоугольного ∆ АОВ по т.Пифагора АО=√(АВ²+ОВ²)=√(0,64+0,36)=0,4 (см)

AD=CD+CA=1,2+0,4=1,6 (см)