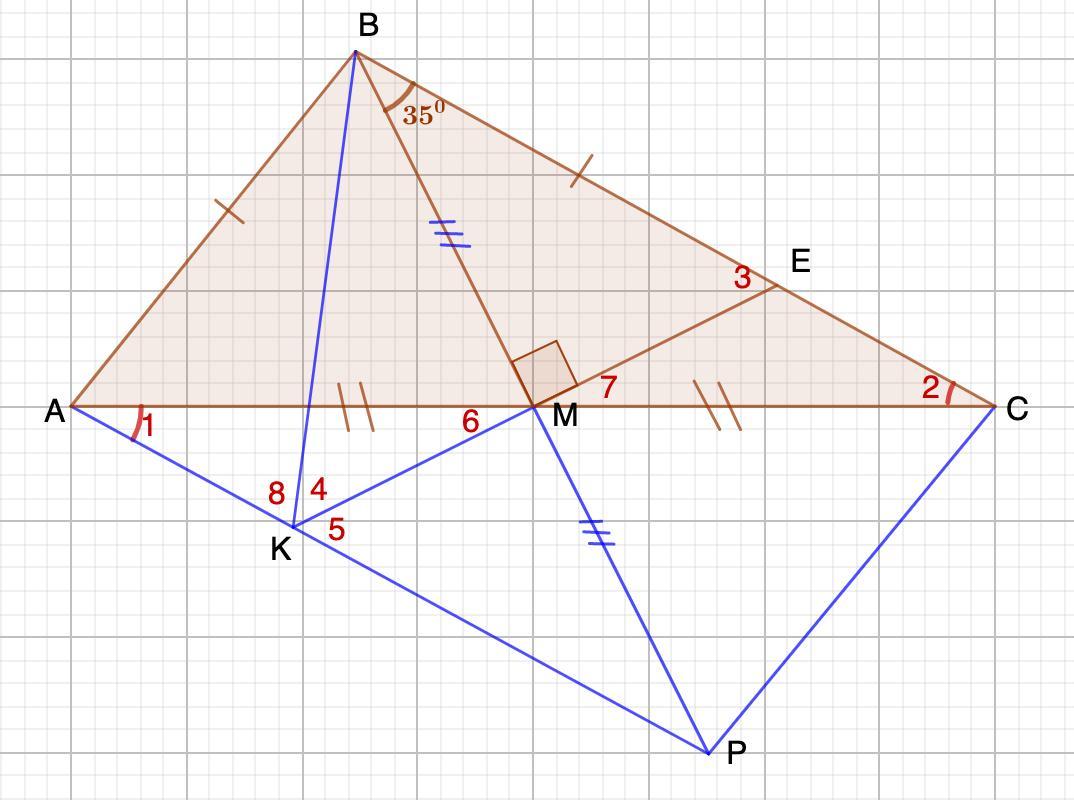
в треугольнике ABC провели медиану BM. на его строне BC взяли точку E так, что угол BME прямой. известно, что AB =BE, а угол MBE = 35 °.найдите угол ABC
Ответы
Ответ:
110°
Объяснение:
Дано: ΔАВС
ВМ - медиана; ∠ВМЕ = 90°; АВ=ВЕ; ∠МВЕ = 35°
Найти: ∠АВС
Решение:
Дополнительное построение: ВМ=МР;
Соединим А и С с Р. Продолжим МЕ до пересечения с АР.
1. Рассмотрим ΔВМЕ - прямоугольный.
∠3=90°-35°=55° (сумма острых углов п/у треугольника)
2. Рассмотрим ΔАМР и ΔВМС.
АМ=МС (условие); ВМ=МР (построение)
∠АМР=∠ВМС (вертикальные)
⇒ ΔАМР = ΔВМС (по 1 признаку)
⇒ ∠1=∠2(соответственные элементы)
3. Рассмотрим ΔАМК и ΔМЕС.
АМ=МС (условие); ∠1=∠2 (п.2); ∠6=∠7 (вертикальные)
⇒ ΔАМК = ΔМЕС (по 2 признаку)
⇒ КМ=МЕ (соответственные элементы)
4. Рассмотрим ΔКВЕ.
КМ=МЕ (п.3); ВМ⊥КЕ (условие)
⇒ВМ - медиана, высота.
⇒ ΔКВЕ - равнобедренный
⇒∠3=∠4=55° (при основании р/б треугольника)
5. ∠1=∠2 (п.2) = накрест лежащие при АР и ВС и секущей АС
⇒ АР ║ ВС
⇒ ∠3=∠5=55° (накрест лежащие при АР ║ ВС и секущей КЕ)
⇒∠8 = 180°-(55°+55°)=70° (развернутый)
6. Рассмотрим ΔАВК.
АВ=ВЕ (условие)
КВ=ВЕ (ΔКВЕ - равнобедренный)
⇒ АВ=КВ ⇒ ΔАВК - равнобедренный ⇒∠8=∠А = 70° (при основании р/б треугольника)
∠АВК = 180°-(70°+70°)=40° (сумма углов треугольника.)
7.∠КВМ=∠МВЕ=35° (ΔКВЕ - равнобедренный)
∠АВС=∠КВМ+∠МВЕ+∠АВК=35°+35°+40°=110°