Предмет: Алгебра,
автор: esstry
СРОЧНО. Найти 7 производных. С решением, пожалуйста.
Приложения:
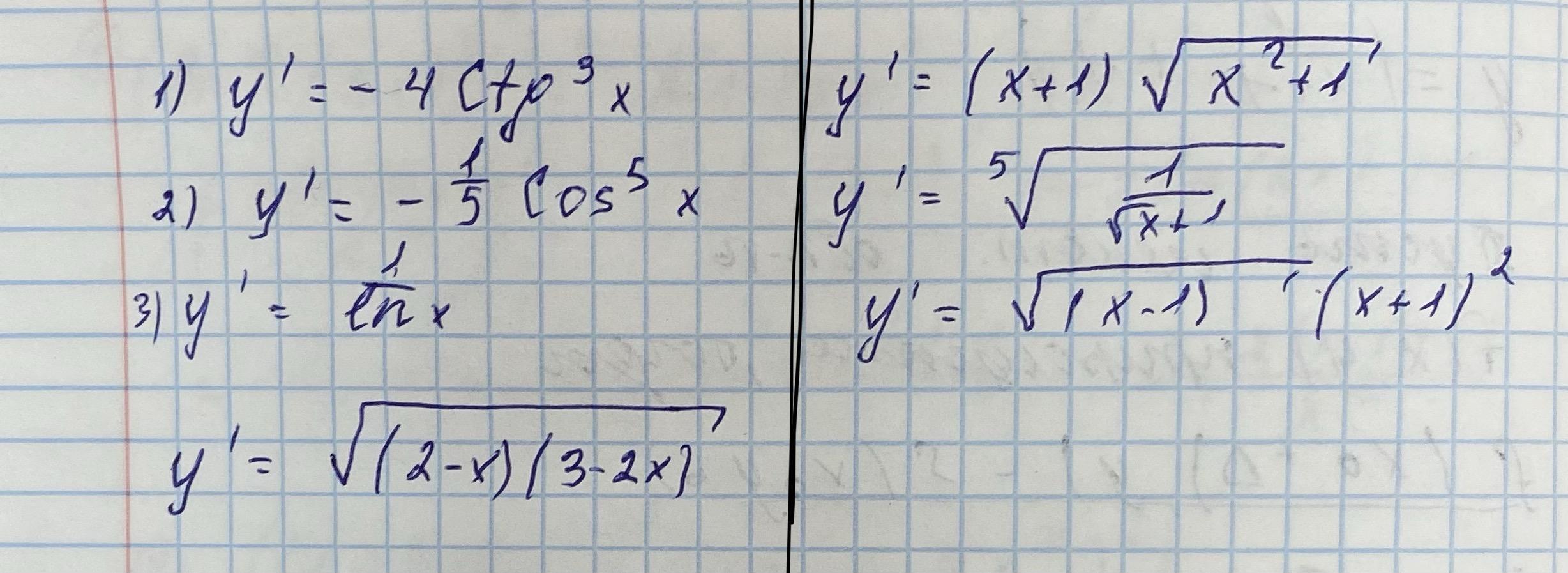
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Українська мова,
автор: karikari1
Предмет: Английский язык,
автор: karakat09
Предмет: Английский язык,
автор: Капр11
Предмет: Алгебра,
автор: ira16540iraaaa
Предмет: Математика,
автор: zzzzz555551
Помоги,пожалуйста