Предмет: Алгебра,
автор: esstry
СРОЧНО. Найти 7 производных. С решением пожалуйста.
Приложения:
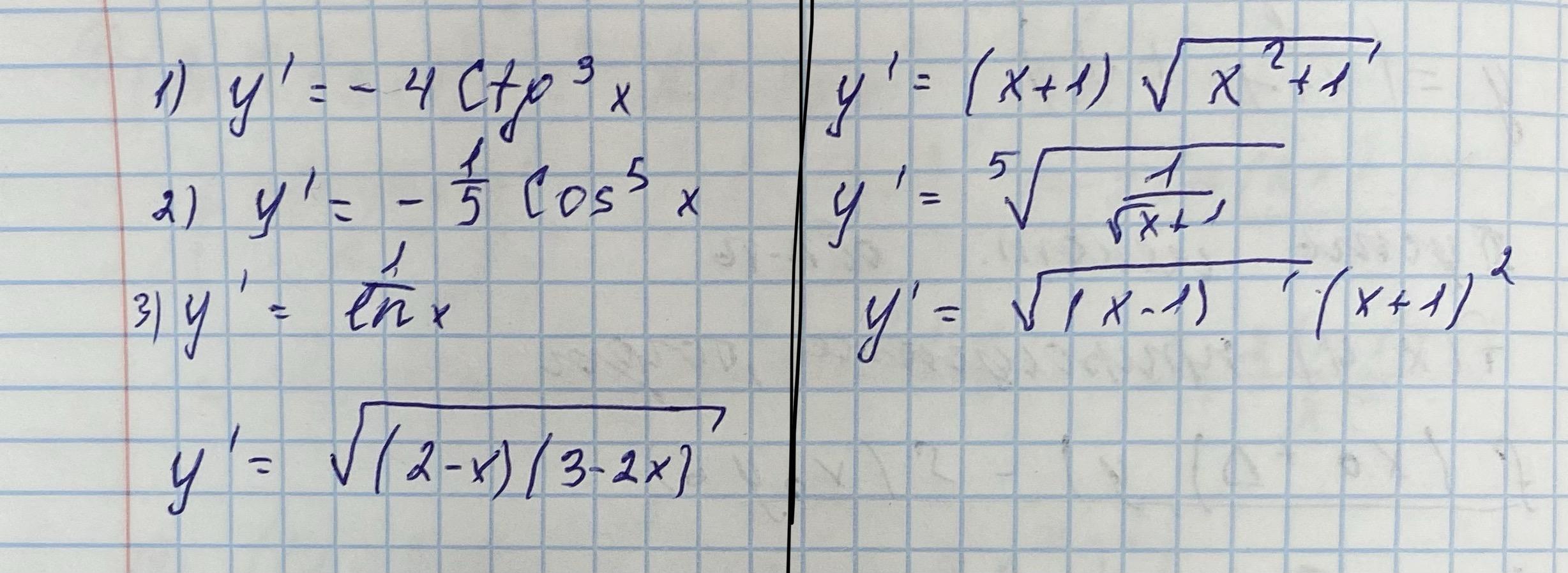
Ответы
Автор ответа:
0
Объяснение:
1)
2)
3)
4)
5)
6)
7)
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Баалберит
Предмет: Русский язык,
автор: суперксеничка
Предмет: Химия,
автор: markusplay
Предмет: Русский язык,
автор: markioscom2p69m9g