Предмет: Алгебра,
автор: mnnkl
Объясните, что уравнение не имеет корня. Помогите!
Приложения:
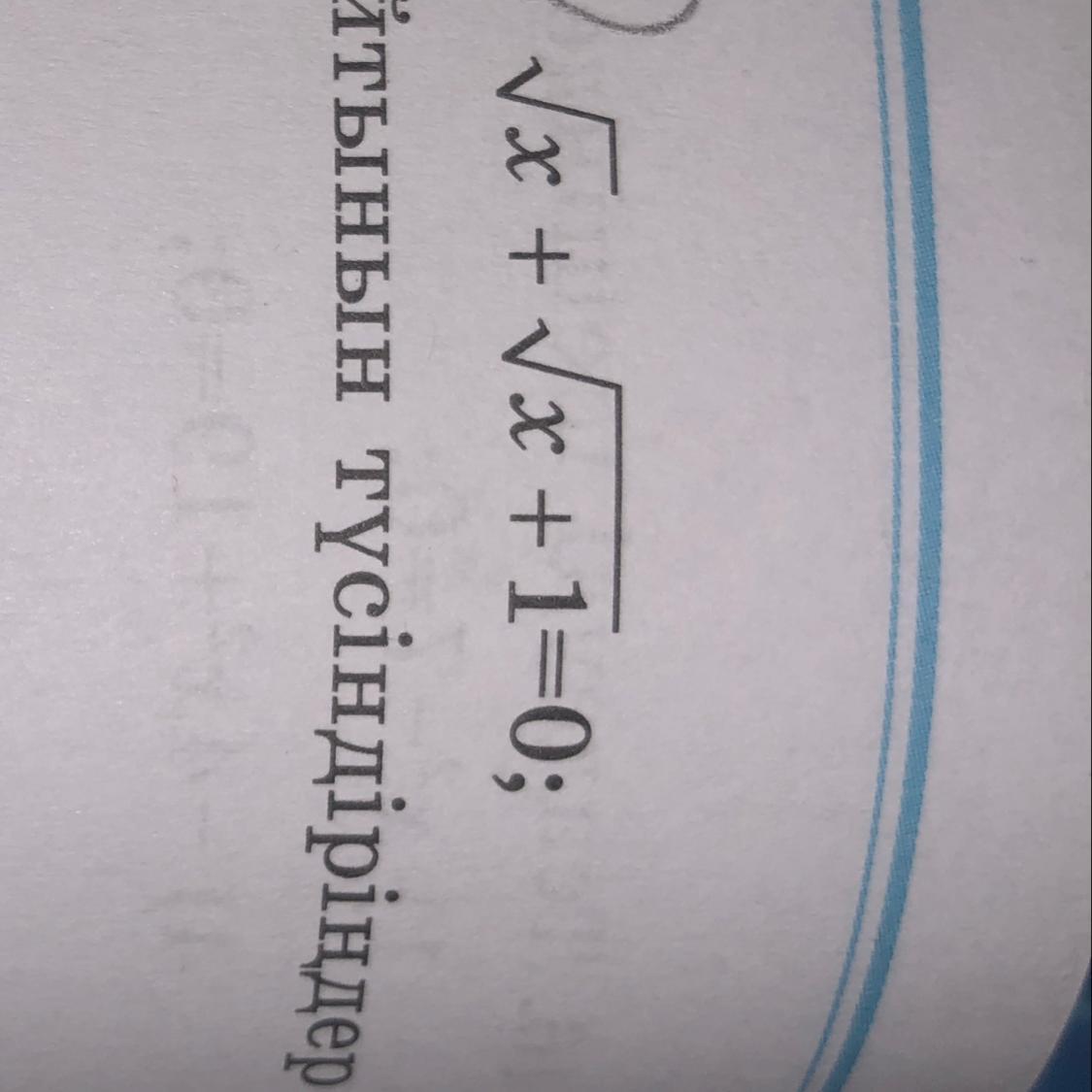
Ответы
Автор ответа:
1
Ответ: x∈∅
Объяснение:
Умножим обе части уравнения на ( ). Тогда левую часть можно будет разложить по формуле разности квадратов : (a + b)(a - b) = a² - b² ; а правая часть так и останется равнa нулю (произведение чисел, из которых хотя бы одно – 0, всегда даст 0). Далее, мы находим, что числовое равенство оказывается неистинным, а значит уравнение не имеет корней.
x ∈ ∅
TomasSmZRs:
Это как один из вариантов решения. Другой заключается в том, чтобы перенести √(х+1) в правую часть уравнения, и далее возвести обе части в квадрат. Получилось бы (х = х+1) => 0 = 1, что также ложно.
Похожие вопросы
Предмет: Английский язык,
автор: 1234543217
Предмет: Русский язык,
автор: vecz6776
Предмет: Русский язык,
автор: помогуипомоги1
Предмет: Другие предметы,
автор: Lika3921
Предмет: Биология,
автор: lemuro4kaovt2gn