Question

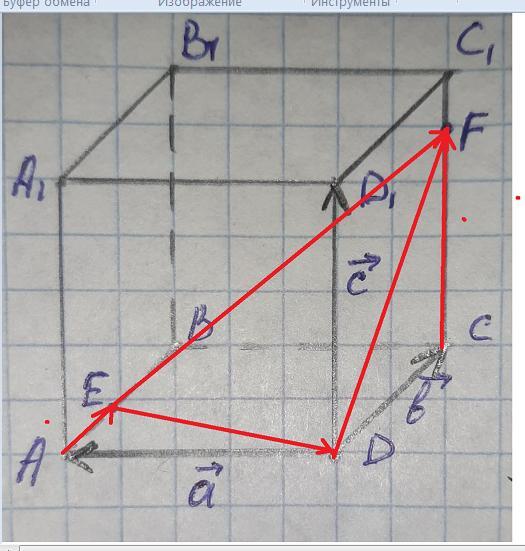
Три некомпланарных вектора a→, b→ и c→ размещены на рёбрах куба с общей вершиной. Точка E делит ребро AB так, что AE:EB=1:1, а точка F делит ребро CC1 так, что CF:FC1=3:2

Разложи по векторам a→, b→ и c→ векторы DE→ и EF→.
(Ответ округляй до сотых.)
DE→ = □a→ + □b→ + □c→;
EF→ = □a→ + □b→ + □c→.

Помогите, пожалуйста, я уже несколько видеороликов посмотрела по этой теме, никак не могу понять, как решить это задание.


​

Answer 1

CF = (3/5) CC1 = (3/5)DD1 = (3/5)c.

Векторы: DF = b + (3/5)c.

                AE = (1/2)b.

               DE = a + AE = a + (1/2)b.

               EF = ED + DF = -DE + DF = -a - (1/2)b + b + (3/5)c =

                    =  -a + (1/2)b + (3/5)c.