Предмет: Алгебра,
автор: Likeeo
ПОМОГИТЕ РЕШИТЬ СРОЧНО 5-6-7!!!
Приложения:
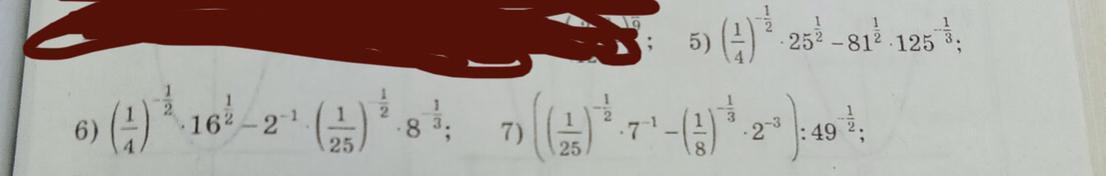
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: NADRAV1
Предмет: Окружающий мир,
автор: ejyvak
Предмет: Русский язык,
автор: Ovharka
Предмет: Геометрия,
автор: Основа2009
Предмет: Химия,
автор: moiseenkovvlad