Question

Даю 35 баллов!
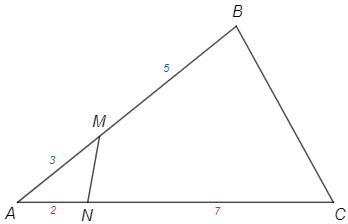
На сторонах AB и AC треугольника ABC выбрали точку M и точку N так, чтобы AM/MB=3/5 , AN/NC= 2/7. Найти площадь четырёхуг. MBCN если площадь треуг. AMN =36​

Answer 1

Площади треугольников с равным углом относятся как произведения прилежащих углу сторон (следует из формулы S =1/2 ab sinC).

S(AMN)/S(ABC) =AM*AN/AB*AC =AM/AB *AN/AC =3/8 *2/9 =1/12

S(AMN)/S(MBCN) =1/11 => S(MBCN) =36*11 =396

Answer 2

Рассмотрим треугольники AMB и ABC.

У них общий угол А и задано соотношение сторон.

Пусть их площади равны соответственно S1 и S2.

Примем коэффициенты пропорциональности по стороне АС за х, по стороне АВ за у.

S1 = (1/2)*2x*3y*sin A.

S2 = (1/2)*9x*8y*sin A.

Разделим первое уравнение на второе.

S1 /S1 = 1/12.

Отсюда получаем ответ: площадь четырёхугольника MBCN равна

S(MBCN) = 36*(12 - 1) = 396 кв.ед.