Question

ПОМОГИТЕ СРЧНО 25 БАЛЛЛОООВВВВ ДАМ СРОЧНО

Answer 1

Ответ:

$(\sqrt{6} ;\frac{91}{7} )$ и $(-4,7; \frac{91}{7})$.

Объяснение:

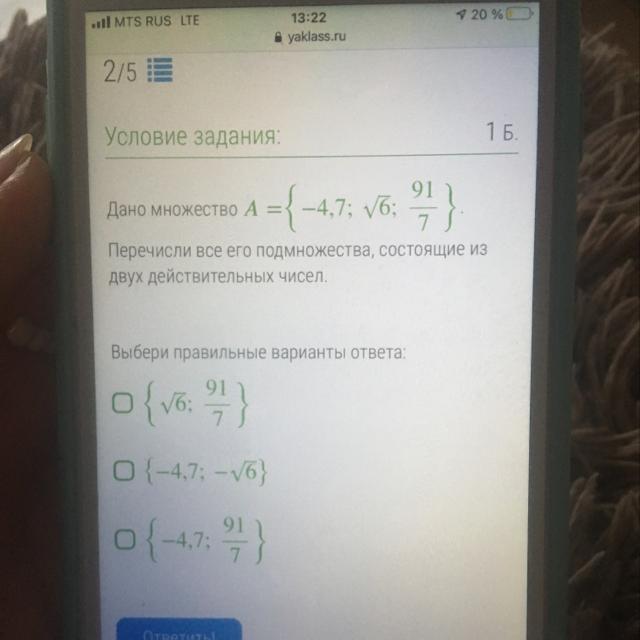
Нам дано множество $A=(-4,7; \sqrt{6};\frac{91}{7})$, требуется перечислить все его подмножетсва, состоящие из двух действительных чисел.

Множество действительных чисел, это совместное множество рациональных и иррациональных чисел, другими словами, это множество чисел (-∞; +∞).

Рациональные числа, это те числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби, или нулем. Из нашего множества, рациональными числами являются числа: $-4,7; \frac{91}{7}$, хоть дробь $\frac{91}{7}$ делится без остатка и может быть представлена в виде целого числа 13, но так как она записана в виде дроби, то это в первую очередь рациональное число.

Иррациональные числа, это такие числа, которые невозможно представить в виде деления двух целых чисел, то есть в виде дроби рационального числа. Это все числа, которые выражаются бесконечными дробями. Из нашего множества A к иррациональным числам относится $\sqrt{6}$, который будет бесконечной дробью.

Я расписал все это для того, чтобы доказать, что все числа множества А являются действительными числами.

Поэтому из нашего множества А можно собрать три подмножества, состоящих из двух чисел:

$(-4,7;\sqrt{6}); (-4,7; \frac{91}{7}); (\sqrt{6} ;\frac{91}{7} )$

Теперь посмотрим на варианты ответов, из них под допустимые подмножества подходят только первый и третий варианты: $(\sqrt{6} ;\frac{91}{7} )$ и $(-4,7; \frac{91}{7})$. Второй вариант не подходит, так как число $-\sqrt{6}$ не является множеством А.