Предмет: Алгебра,
автор: ymk5yvczz7
решите логарифмическое неравенство, пожалуйста
Приложения:
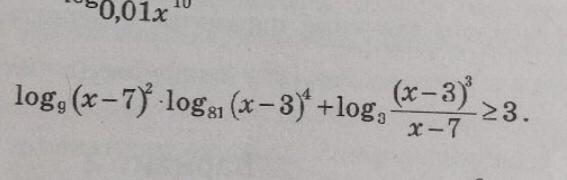
Ответы
Автор ответа:
3
Объяснение:
ОДЗ:
-∞__+__3__-__7__+__+∞
x∈(-∞;3)U(7;+∞).
1. x∈(7;+∞).
2. x∈(-∞;3).
Ответ: x∈(-∞;0]U[7¹/₂₇;+∞).
Автор ответа:
4
Ответ:
Объяснение:
............................................
Приложения:
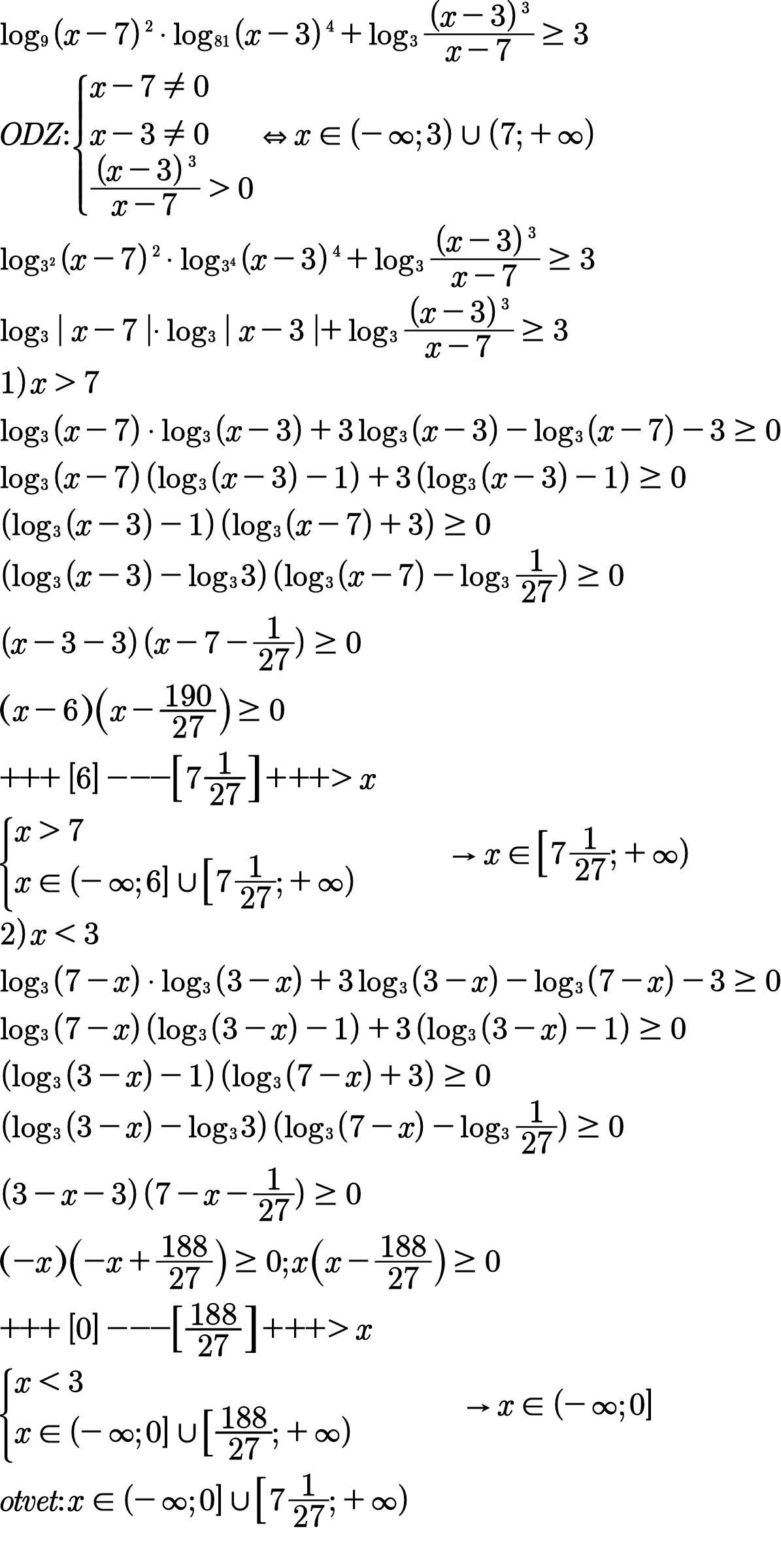
Похожие вопросы
Предмет: Русский язык,
автор: Оля200290
Предмет: Английский язык,
автор: Gospog
Предмет: Русский язык,
автор: двочник
Предмет: Математика,
автор: 1777Котик7771
Предмет: Окружающий мир,
автор: dantes6