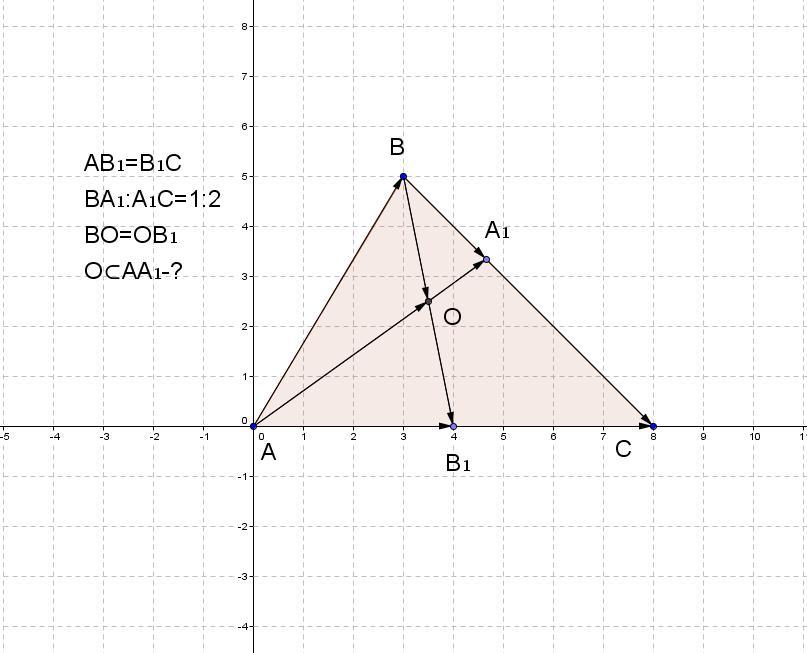
В треугольнике АВС В1-середина АС, точка А1 лежит на стороне ВС так, что ВА1 : А1С = 1 : 2. Используя векторы, докажите, что середина ВВ1 лежит на прямой АА1
Ответы
Ответ:
Объяснение:
Изменю некоторые буквы условия. Написание индексов напрягает здесь.
В треугольнике ABC точка E-середина АС, точка F лежит на стороне BC так, что BF : FC = 1 : 2. Используя векторы, докажите, что середина BE лежит на прямой AF.
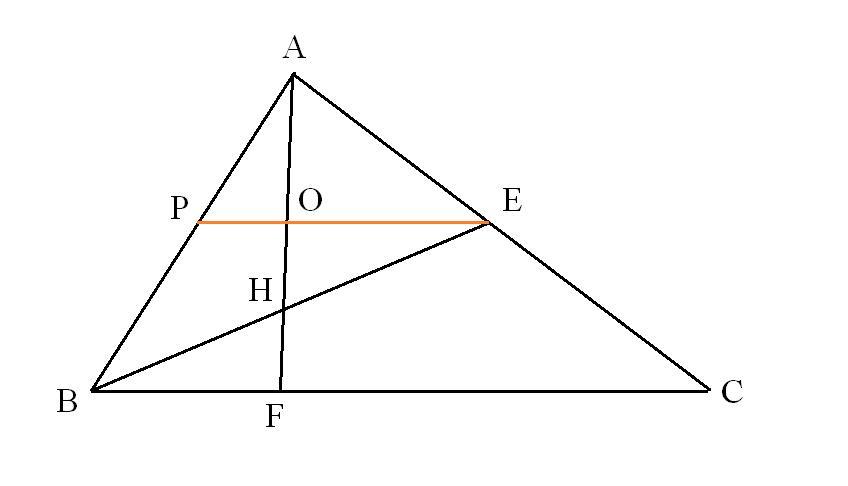
Достроим среднюю линию EP||BC
EP∩AF=O; BE∩AF=H.
Докажем, что BH=HE
PE||BC⇒ΔAPO~ΔABF, ΔAOE~AFC, ΔAPE~ΔABC с одним и тем же коэффициентом подобия k=0,5
Тогда
PO=0,5BF=0,5(0,5FC)=0,5OE⇒PO=0,5OE
Рассмотрим ΔABE
EP-медиана, OE=2PO⇒AH-медиана.
ч.т.д.
Ответ:
////////////////
Объяснение:
поместим точку А в начало прямоугольной системы координат, а точку С - на оси Х
примем направления векторов, как показано на рисунке 1
докажем, что вектор АО→ коллинеарен вектору АА₁→, а поскольку они имеют общую точку А, то и точка О (середина вектора ВВ₁→) лежит на прямой АА₁