Предмет: Алгебра,
автор: Miа16
Алгебра. Даю 10 баллов. Решить 2 уравнения. С подробным решением.
Приложения:
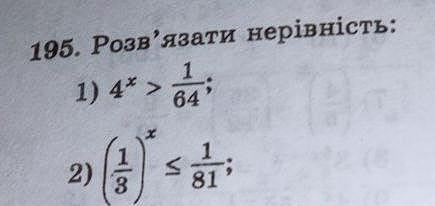
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Приравниваем основания в одно число и просто отбрасываем
///////////
-------o---------->x
-3
Ответ: x ∈ (-3;+∞)
как уже понятно со вторым тож самое
тут 1 в 4 степени равен 1 поэтому вынесли степень за скобки
///////////
-------*--------->x
4
Ответ: x ∈ [4;+∞)
или
тут есть такая система х)
легче да? ну в смысле понять
4585o7k5099:
да уже....
"тут 1 в 4 степени равен 1 поэтому вынесли степень за скобки"
ничего непонятно
почему стало больше равно ?
ничего непонятно
почему стало больше равно ?
Там 1 в 4 степени ты понял, а вот почему больше равно внизу есть другая система решения где показано почему, а так это из за дроби
я же сказал из за дроби
+ я решил 2 способами, а если вы не понимаете, я не виноват
во втором способе ясно видно что уравнение я умножил на (-1) и поменял знак
Ответ: x ∈ [4;+∞)
или
тут есть такая система х)
легче да? ну в смысле понять
или
тут есть такая система х)
легче да? ну в смысле понять
Похожие вопросы
Предмет: Окружающий мир,
автор: vikalokteva06
Предмет: Английский язык,
автор: pers3
Предмет: Русский язык,
автор: таня692
Предмет: Экономика,
автор: Аноним
Предмет: Химия,
автор: kariccc