Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, срочно!
Вычислить несобственный интеграл или установить его расходимость.
Приложения:
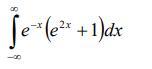
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: mikka1
Предмет: Русский язык,
автор: saky09
Предмет: Английский язык,
автор: irinakrylos
Предмет: Математика,
автор: manassaakyan777
Предмет: Обществознание,
автор: Aysu2004