Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, срочно!
Исследовать непрерывность функции f (x). Найти точки разрыва функции и
определить их характер. Выполнить геометрическую иллюстрацию.
Приложения:
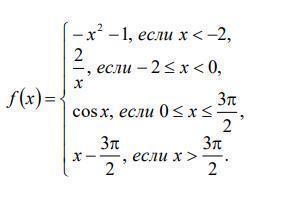
Ответы
Автор ответа:
1
Ответ:
Функция при х= -2 имеет разрыв 1 рода . Скачок равен -1-(-5)=4 .
При х=0 функция имеет разрыв 2 рода .
При функция непрерывна .
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: мама53я
Предмет: Русский язык,
автор: Алмагуль1
Предмет: Окружающий мир,
автор: vika0289111
Предмет: Алгебра,
автор: pipboy2