Предмет: Алгебра,
автор: annpop17
алгебра 11 класс 50 баллов
Приложения:
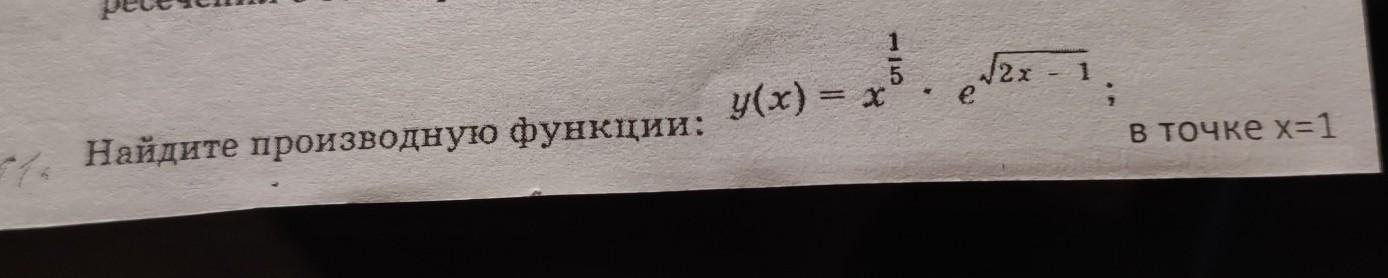
Ответы
Автор ответа:
1
Объяснение:
x=1
annpop17:
спасибо, но уже решил сам
там в ответе подстановка еще
Похожие вопросы
Предмет: Окружающий мир,
автор: shuha1
Предмет: Русский язык,
автор: Ksushaknish
Предмет: Русский язык,
автор: крюха12345678909
Предмет: История,
автор: Аноним
Предмет: Русский язык,
автор: Алина407і156