Предмет: Алгебра,
автор: dzubaviktoria21
Поможіть пжжжжжж
.
.
.
Приложения:
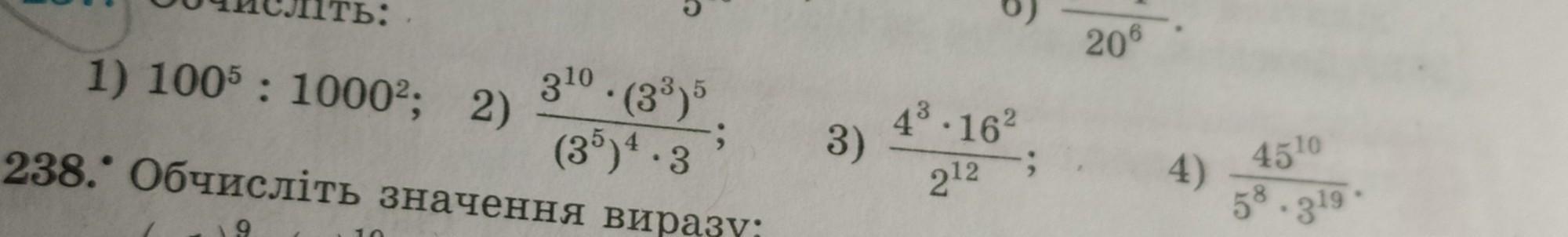
Ответы
Автор ответа:
0
Ответ:
Объяснение:
• Произведение двух степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным сумме показателей множителей:
• Частное двух степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным разности показателей делимого и делителя:
• При возведении степени в степень основание оставляют тем же, а показатели перемножают:
Похожие вопросы
Предмет: Русский язык,
автор: Vekmpz3489
Предмет: Қазақ тiлi,
автор: қурай
Предмет: Английский язык,
автор: дашуля177
Предмет: Литература,
автор: Moonnightaiym
Предмет: Геометрия,
автор: Vladislavalk