Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, срочно!
Вычислить интеграл
Приложения:
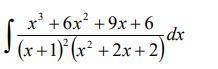
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: Yukihyo
Предмет: Английский язык,
автор: тик9
Предмет: Другие предметы,
автор: катя1709
Предмет: Математика,
автор: лола2610