Предмет: Геометрия,
автор: 1307A
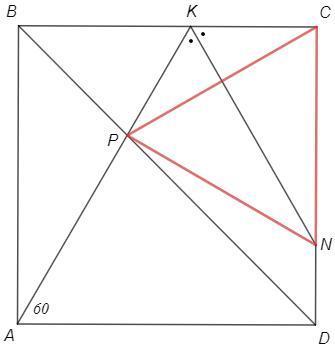
На стороне ВС квадрата АВСD взята точка К такая, что угол KAD=60 градус . Отрезок КА пересекает диагональ ВD в точке Р, а биссектриса угла СКА пересекает сторону СD в точке N. Докажите, что треугольник СРN – равносторонний.
Ответы
Автор ответа:
1
Квадрат симметричен относительно диагонали.
∠PAD=∠PCD=60 (симметрия) //или △ADP=△CDP по двум сторонам и углу между ними
∠AKC=180-∠KAD=120 (внутренние односторонние при параллельных)
∠PKN =120/2=60
Отрезок PN виден из K и С под равным углом => PKCN - вписанный
=> ∠PNC =180-∠PKC =60
∠PCN=∠PNC=60 => △CPN - равносторонний
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: ирина419
Предмет: Окружающий мир,
автор: enyashina1
Предмет: Русский язык,
автор: mail79
Предмет: Английский язык,
автор: милентос