Предмет: Математика,
автор: Jokerdjd
помогите , решить пожалуйста
Приложения:
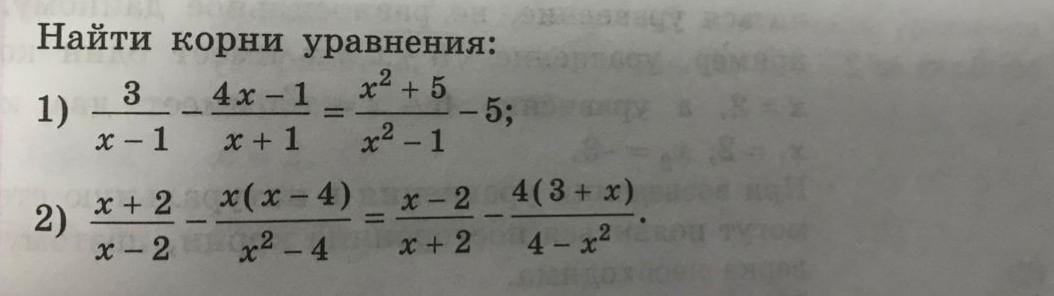
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1)
Поскольку выражение имеет смысл , если знаменатель не равен 0 , значит х не может быть равен :
х - 1 ≠ 0
х ≠ 1
х + 1 ≠ 0
х ≠ -1
х² - 1 ≠0
х² ≠ 1
х ≠ ±1
Получаем , что при х = 1 - выражение не имеет смысл , следовательно у этого уравнения нет корней.
2)
Наше выражение будет иметь смысл если :
х ≠ ± 2 , значит корень х = 2 - не подходит .
Корнем уравнения будет :
х = 6
Похожие вопросы
Предмет: Английский язык,
автор: masta163
Предмет: Русский язык,
автор: alsu8612
Предмет: Русский язык,
автор: vika2003oleg222
Предмет: История,
автор: kirill3191daynp6z0st
Предмет: Окружающий мир,
автор: Миха1212