Question

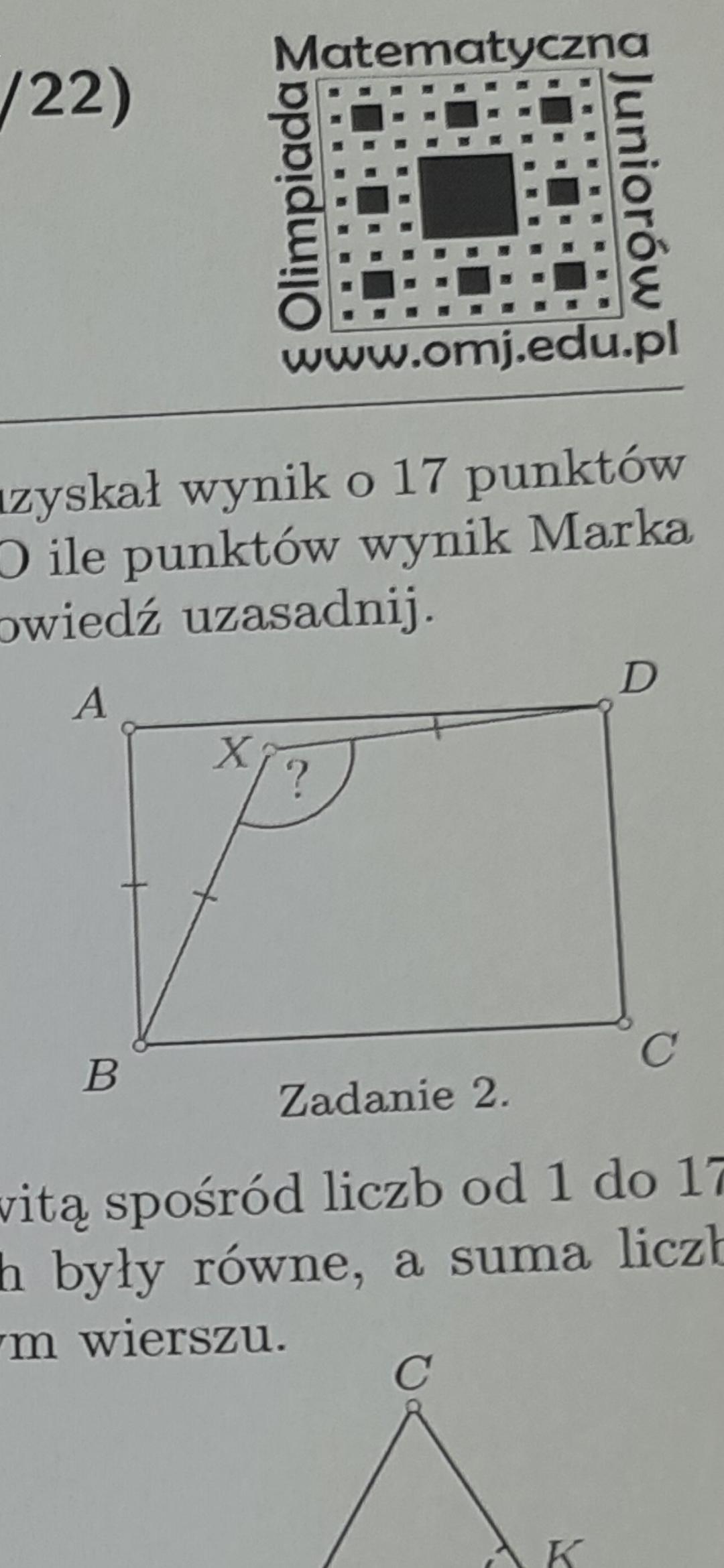
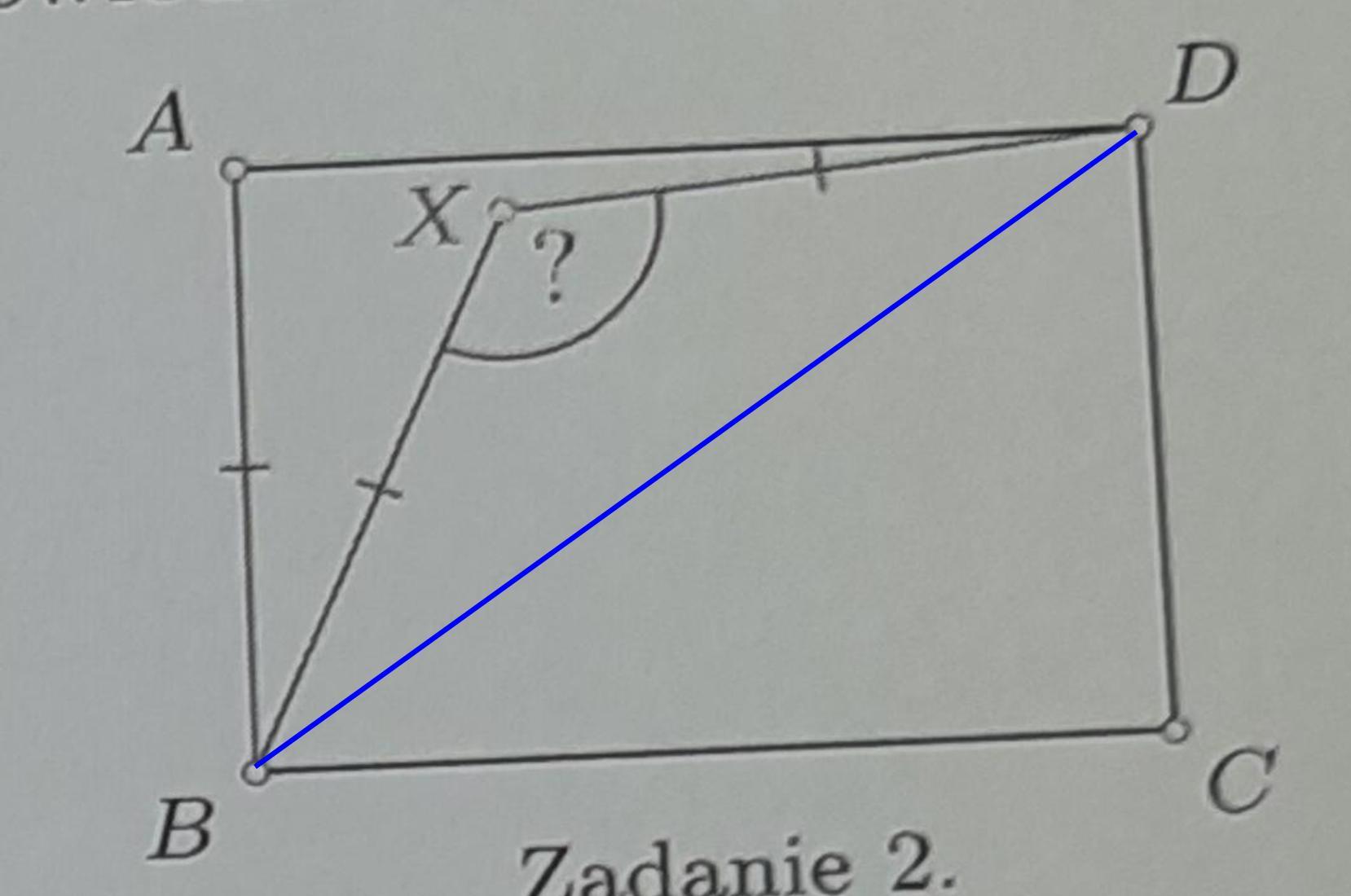
2. В прямоугольнике ABCD отношение длин сторон BC: AB равно корню из 2. Внутри прямоугольника отмечена точка X так, что AB = BX = XD. Найдите угловую меру BXD.

Answer 1

1) AB = CD

   AD = BC как противоположные стороны прямоугольника АВСD.

2) Пусть СD = х, тогда ВС = х√2.

По тереме Пифагора найдем ВD - диагональ прямоугольника.

ВD² = СD² + ВС²

ВD² = х² + (х√2)²

ВD² = 3х²

ВD = х√3

3) По условию АВ = ВХ = ХD    =>   ВХ = ХD = x.

4) Для ΔВХD применим теорему косинусов.

ВD² = ВХ² + ХD² - 2 · ВХ · ХD ·cos∠BXD

(x√3)² = x² + x² - 2·x·x·cos∠BXD

3x² = 2x² - 2x²· cos∠BXD

2x²·cos∠BXD = -3x² + 2x²

2x² ·cos∠BXD = - x²

cos∠BXD = $\frac{-x^{2} }{2x^{2} } =-\frac{1}{2}$

cos∠BXD =  $-\frac{1}{2}$      =>     ∠BXD = 120°

Ответ: 120°