Предмет: Алгебра,
автор: anastasia063rus
Пожалуйста! Нужно полное решение. Найти производную функций:
Приложения:
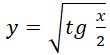
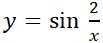
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: кира1235
Предмет: Английский язык,
автор: maksimenko41
Предмет: Физика,
автор: vladislavab04
Предмет: Қазақ тiлi,
автор: UltraSU