Предмет: Алгебра,
автор: Аноним
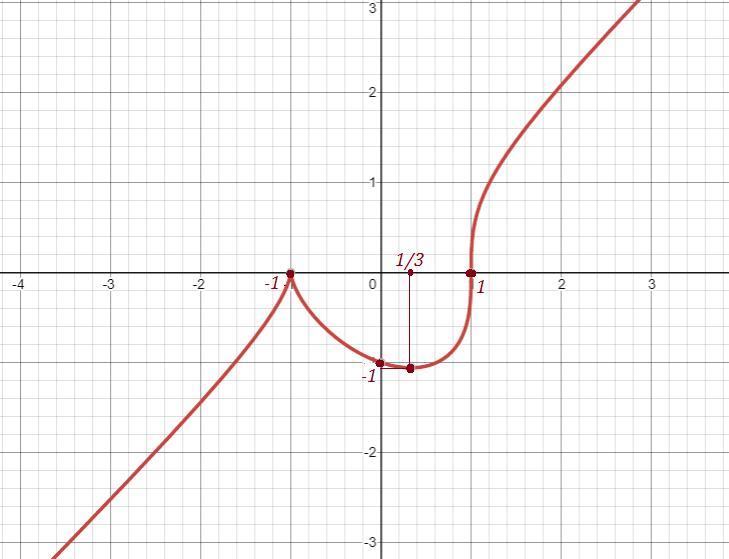
интервалы возрастания и убывания
Приложения:
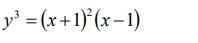
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: дима834
Предмет: Английский язык,
автор: ника2911
Предмет: Английский язык,
автор: katya300887
Предмет: Химия,
автор: oljik434
Предмет: Литература,
автор: masha22123129