Предмет: Математика,
автор: lavrovkolea06
Решите систему уравнений, используя способ сложения:
Приложения:
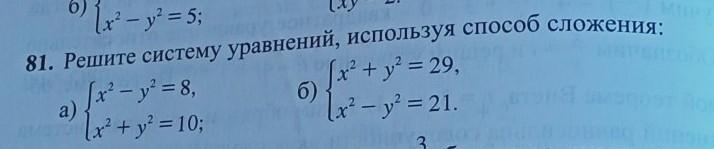
Ответы
Автор ответа:
1
Пошаговое объяснение:
а)
Почленно сложим уравнения :
Подставим значение х в любое из уравнений и найдем значение у.
При х₁ = 3
При х₂ = -3
Решением системы является : ( 3:1) ; ( 3 ; -1) ; (-3; 1) ; (-3; -1)
Ответ : ( 3:1) ; ( 3 ; -1) ; (-3; 1) ; (-3; -1)
б)
Почленно сложим уравнения :
Подставим значение х в любое из уравнений и найдем значение у.
При х₁ = 5
При х₂ = -5
Решением системы является : ( 5;2) ; ( 5; -2) ; (-5;2) ; (-5; -2)
Ответ : ( 5;2) ; ( 5; -2) ; (-5;2) ; (-5; -2)
lavrovkolea06:
огромное спасибо ✊
Похожие вопросы
Предмет: Английский язык,
автор: мадик10
Предмет: Қазақ тiлi,
автор: makslmus2002111
Предмет: Английский язык,
автор: azaromeo
Предмет: Математика,
автор: KatyLala
Предмет: Математика,
автор: Аноним