Предмет: Алгебра,
автор: shumkogleb39
сокращение рациональных дробей
Приложения:
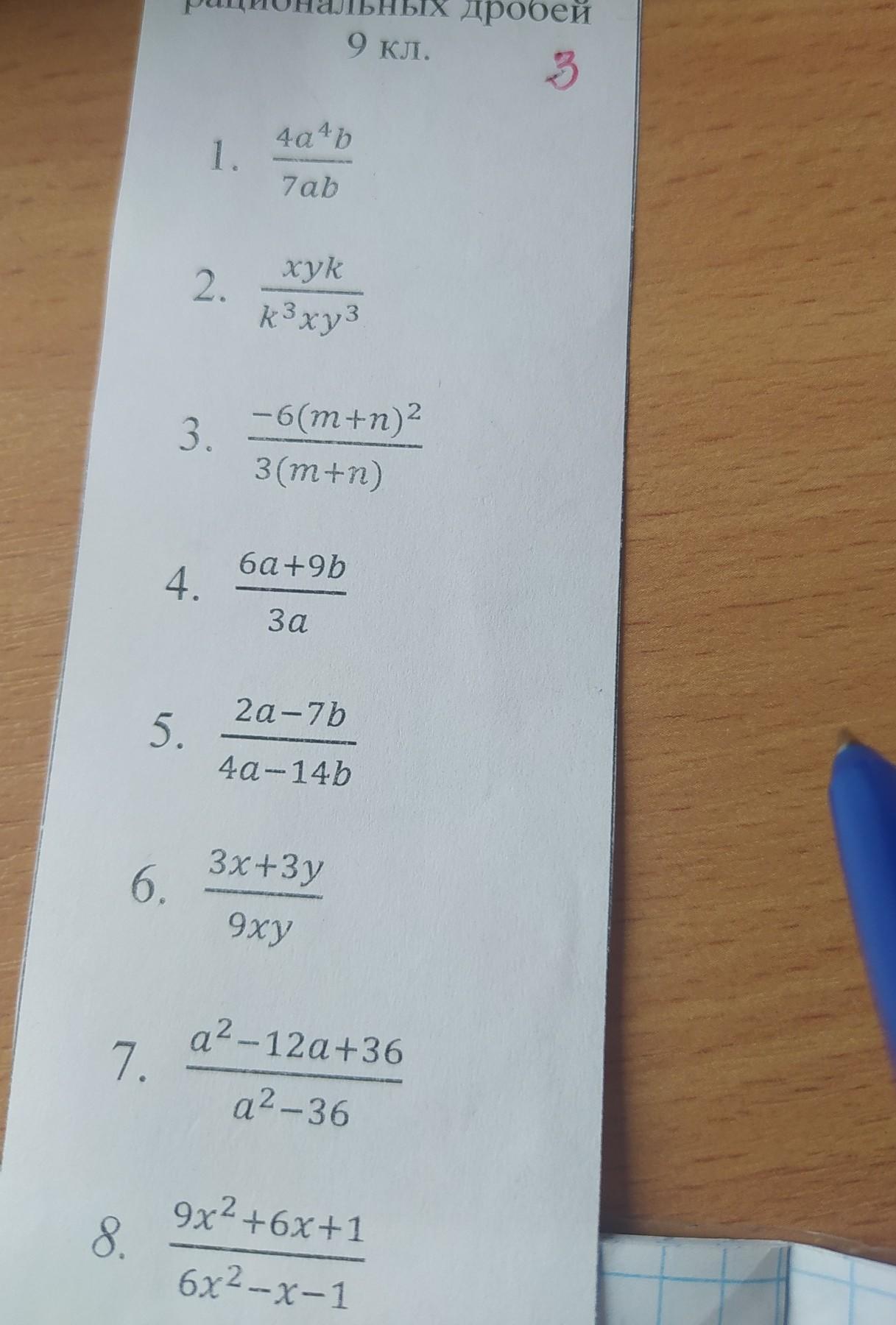
Ответы
Автор ответа:
0
1.
2.
3.
4.
5.
6.
7.
8.
Разложение на множители:
Похожие вопросы
Предмет: Английский язык,
автор: dany1927
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Ruslan111111110
Предмет: Алгебра,
автор: ulama2924
Предмет: Биология,
автор: maksdh