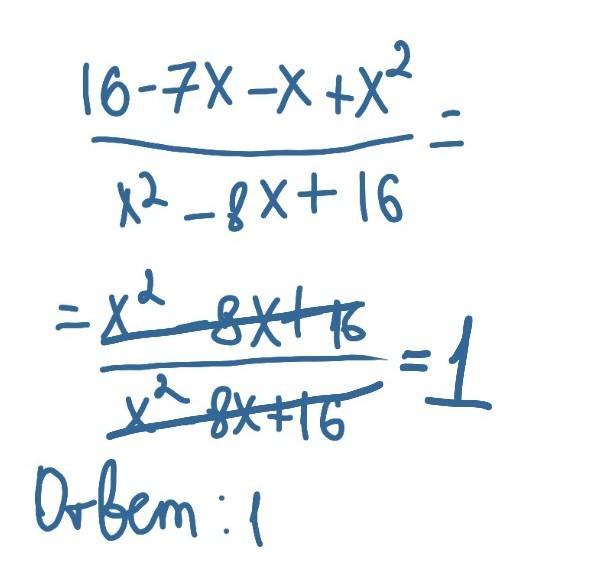Помогите пожалуйста 6 и 7

Ответы
№6
Курсивом я пишу объяснение, просто чтоб было понятно, почему и как так решается. Смотри, у нас знаменатели отличаются только знаком. В первой дроби в знаменателе 6а, а во второй -6а ; в первой дроби в знаменателе -6, а во второй 6. Если мы домножим одну дробь на -1 (у нас и числитель, и знаменатель будет умножаться на минус единицу, потому что при умножении числителя и знаменателя на одно и то же число дробь не меняется), допустим, вторую, то у нас будут знаменатели совпадать. Итак:
Если мы умножим -1 на (6 - 6a), то получим -6 + 6a. А это то же самое, что 6a - 6, то есть теперь у нас равный знаменатель:
Ответ:
№7
Здесь "прикол" в том, что знаменатели обеих дробей раскроются одинаково:
(x - 4)² = x² - 8x + 16
(4 - x)² = 16 - 8x + x²
Поэтому, по сути, у нас общий знаменатель уже есть (круто, правда? Красивый пример:) )
Теперь, поняв это, сложим дроби и раскроем скобки:
(не знаю, почему приложение не даёт мне ещё прикрепить записи, как сверху, поэтому креплю фото)
Ответ: 1