Question

Срочно)))100 баллов!!!!!!

Answer 1

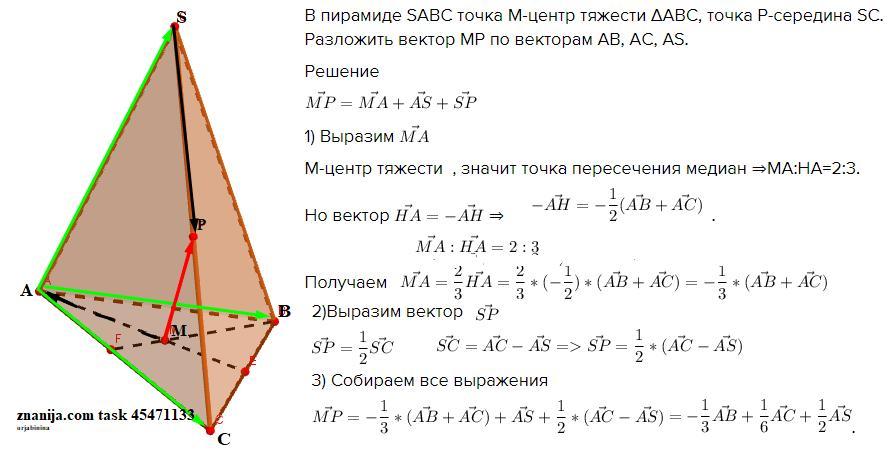
В пирамиде SABC точка М-центр тяжести ΔАВС, точка Р-середина SC. Разложить вектор МР по векторам АВ, АС, AS.

Решение

$\displaystyle \vec {MP} = \vec{MA} +\vec{AS} + \vec{SP}$

1) Выразим $\displaystyle \vec{MA}$

М-центр тяжести  , значит точка пересечения медиан ⇒МА:HA=2:3.

Но вектор $\displaystyle \vec{HA} =- \displaystyle \vec{AH}$ ⇒      $- \displaystyle \vec{AH} =-\frac{1}{2} ( \vec{AB}+ \vec{AC})$  .

Получаем      $\displaystyle \vec{MA} : \vec{HA}=2:3\\ \displaystyle \vec{MA} =\frac{2}{3} \vec{HA} = \frac{2}{3}*(-\frac{1}{2} )* ( \vec{AB}+ \vec{AC})=-\frac{1}{3} * ( \vec{AB}+ \vec{AC})$ .

2)Выразим вектор  $\displaystyle \vec{SP}$

$\displaystyle \vec{SP} =\frac{1}{2} \vec{SC} \\ \displaystyle \vec{SC} =\vec{AC}- \vec{AS} => \displaystyle \vec{SP}=\frac{1}{2} *(\vec{AC}- \vec{AS} )$

3) Собираем все выражения

$\displaystyle \vec{MP} =-\frac{1}{3} * ( \vec{AB}+ \vec{AC})+ \vec{AS}+\displaystyle \frac{1}{2} *(\vec{AC}- \vec{AS} )=$

$\displaystyle =-\frac{1}{3} \vec{AB}+ \frac{1}{6} \vec{AC}+ \frac{1}{2} \vec{AS}$.