Предмет: Алгебра,
автор: asabina07
решите систему уравнений
4х+3=4у^2
3у-х-2=0
Ответы
Автор ответа:
2
asabina07:
спасибо большое
но немного другое мы решаем основную систему с дискриминантом
Автор ответа:
1
Ответ:
4x+3=4y²
x=4y²-3
Объяснение:
ответ получается таким
Приложения:
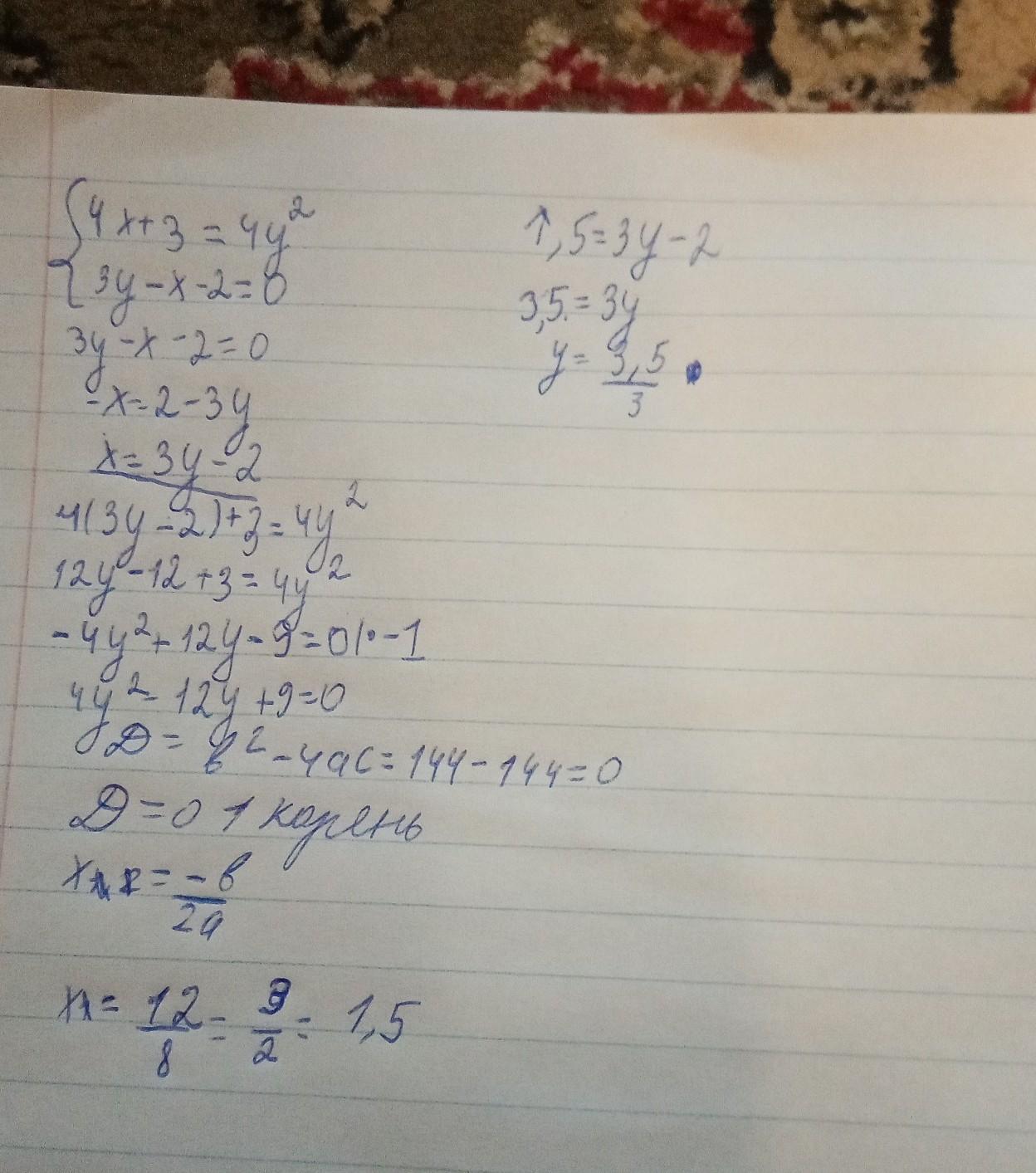
да это точно спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: dana250120
Предмет: Русский язык,
автор: KoteHarote
Предмет: Қазақ тiлi,
автор: ударница01
Предмет: Английский язык,
автор: ludvig9
Предмет: Русский язык,
автор: Юлек111111111111111