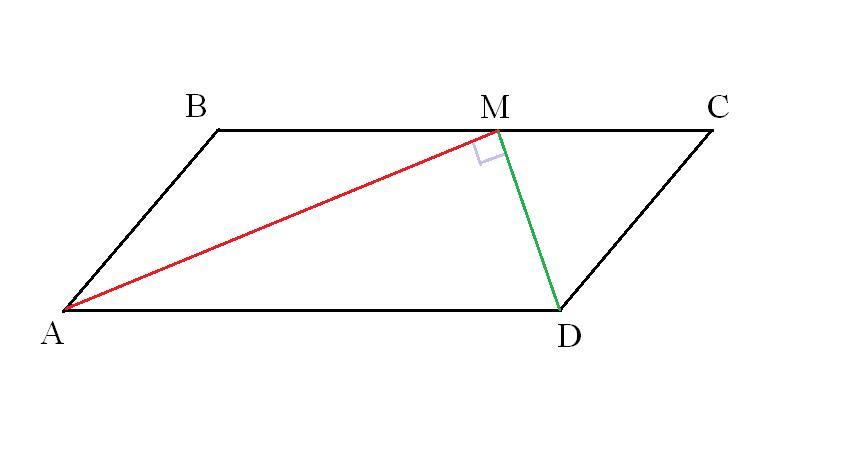
В параллелограмме ABCD биссектриса угла А, равного 60 градусам , пересекает сторону BC в точке M. Отрезки AM и DM перпендикулярны. Найдите периметр параллелограмма , если AB = 10. Еще начертите прошу
ПОМОГИТЕ РАДИ ХРИСТА СРОЧНО НАДО НЕ ШАРЮ НИЧЕГО
Ответы
Ответ:
Объяснение:
Дано: ABCD - параллелограмм
AB=10
∠A=60°
AM⊥DM
AM - биссектриса ∠A
Найти: PABCD = ?
Решение: Т.к AM - биссектриса ∠A, то ∠BAM=∠MAD=60/2=30°
∠MAD=∠BMA (н/л BC║AD и сек. AM (ABCD - параллелограмм) => ΔAMB - р/б по признаку => AB=BM=10
В ΔABM найдем ∠MBA. Сумма углов треугольника равна 180° => ∠MBA+∠BMA+∠MAB=180°
∠MBA=180-∠BMA-∠MAB
∠MBA=180-30-30
∠MBA=120°
Противолежащие углы параллелограмма равны => ∠B=∠D=120°
В ΔAMD - прямоугольном, найдем ∠MDA. Сумма острых углов в прямоугольном Δ равна 90° => ∠MAD+∠MDA=90°
∠MDA=90-∠MAD
∠MDA=90-30
∠MDA=60° => DM - биссектриса ∠D т.к она делит угол пополам
∠MDA=∠DMC=60° (н/л => ΔMDC - равносторонний (третий угол можно посчитать, будет тоже равен 60°) =>MD=MC=CD=10
Найдем BC, а затем периметр:
BC=BM+MC
BC=10+10
BC=20
PABCD=2(AB+BC)
PABCD=2(10+20)
PABCD=60 ед.
Ответ: 60

Ответ:
Объяснение:
1) способ
AM-биссектриса⇒∠BAM=∠MAD=0,5•∠A=30°
ABCD-параллелограмм⇒AB=CD, BC=AD, AD║BC, ∠B=180°-∠A=120°
AD║BC⇒∠BMA=∠MAD=30°⇒∠BMA=∠BAM⇒ΔABM-равнобедренный⇒
⇒MB=AB=10
AM²=AB²+BM²-2AB•BM•cos∠B=10²+10²-2•10•10•cos120°=200+100=300
AM=10√3
AD=AM/cos∠MAD=10√3/cos30°=10√3/(√3/2)=20
P=2(AB+AD)=2(10+20)=60
2) способ
Пересечение прямых AB и DM обозначим точкой E
AM-биссектриса и высота в ΔADE⇒ΔADE- равнобедренный, DM=ME
ΔADE- равнобедренный, ∠A=60°⇒ΔADE- равносторонний⇒AD=AE=DE
DM=ME, BM║AD⇒BM-средняя линия в ΔADE
Из первого способа BM=10
AD=2BM=20