Предмет: Геометрия,
автор: kailoid89
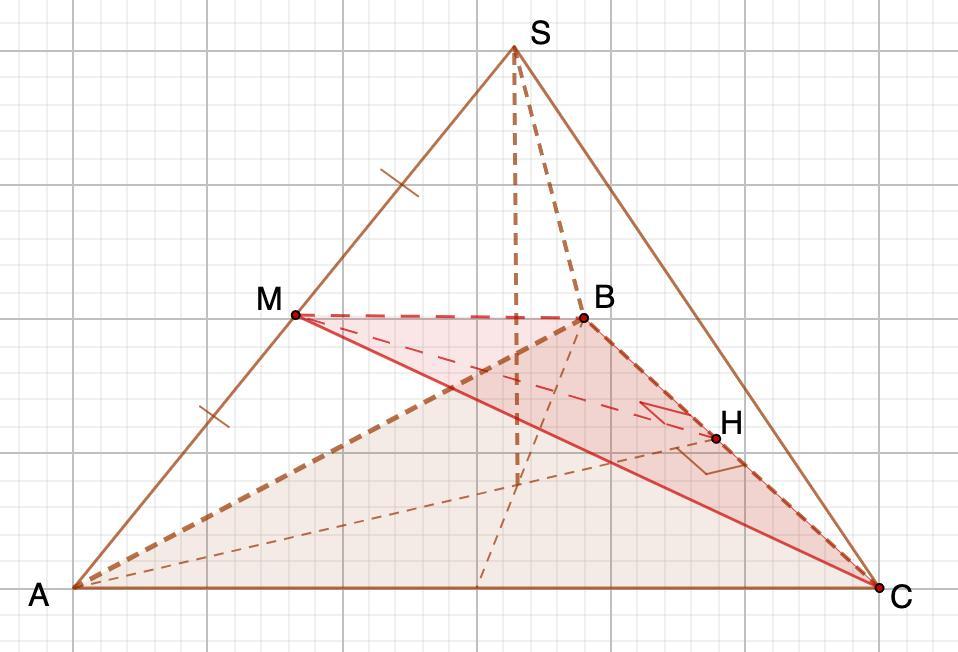
Дана пирамида SABC у которой все ребра равны 1. Точка М - середина ребра SA. Найдите площадь сечения BCM.
Ответы
Автор ответа:
2
Объяснение:
Дано: SABC - пирамида
Все ребра равны 1.
AM=MS
Найти: S (BCM)
Решение:
Если все ребра равны 1, то все грани - равносторонние треугольники.
1. Рассмотрим ΔASC - равносторонний.
СМ - медиана, высота.
2. Рассмотрим ΔАМС - прямоугольный.
АС=1; АМ = 1/2
По теореме Пифагора:
3. Рассмотрим ΔАВС - равносторонний.
АН - высота, медиана.
4. Рассмотрим ΔСМВ - равнобедренный.
МН⊥ВС (теорема о трех перпендикулярах)
⇒ МН - высота, медиана.
5. Рассмотрим ΔСМН - прямоугольный.
По теореме Пифагора:
6.
(ед².)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: iris0102
Предмет: Английский язык,
автор: adil1977
Предмет: Русский язык,
автор: RNatasha181186
Предмет: Химия,
автор: rumyninmv2
Предмет: Геометрия,
автор: никиминажйопта