Предмет: Алгебра,
автор: milkiway0490
Помогите пожалуйста. Задание 1 Найдите производную функции в точке х0=2. Задание 2 вычислите значение производной функции в точке х0=-1
Приложения:
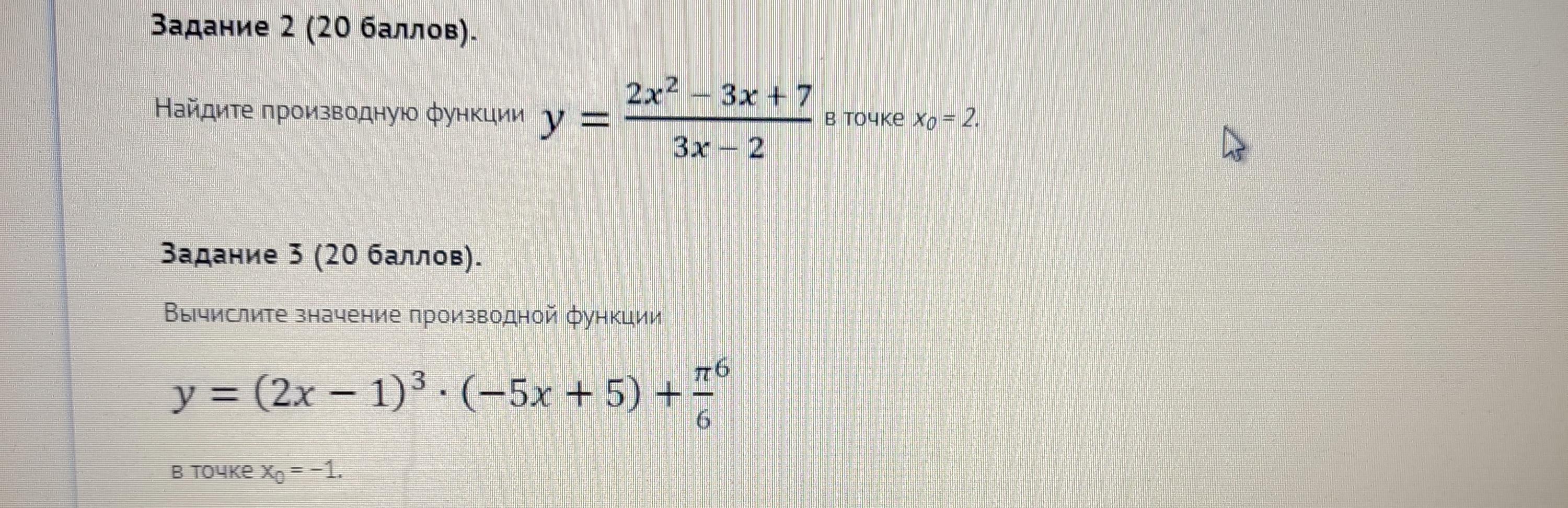
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: лоник1
Предмет: Русский язык,
автор: жуча2
Предмет: Литература,
автор: Masha11781
Предмет: Химия,
автор: lizaaver201357