Предмет: Математика,
автор: MamatvoegoOdnaklasni
Здравствуйте помогите с решением.
Приложения:

Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
для уравнения касательной и нормали нам понадобится первая производная
вот "во первых строках" и найдем эту производную
и еще нам понадобится значение функции и значение производной в точке касания х₀=1
теперь у нас есть все для записи уравнений касательной и нормали
касательная
формула
тогда у нас
нормаль
формула
подставим наши данные
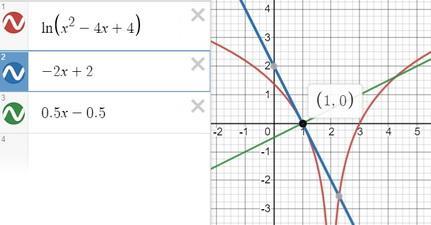
на рисунке
красная - сам график функции
синяя - касательная
зеленая - нормаль
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Dilnura2222
Предмет: Русский язык,
автор: pklevantseva
Предмет: Окружающий мир,
автор: TomDrok09ku
Предмет: Химия,
автор: ksu183
Предмет: Русский язык,
автор: Danek22