Предмет: Математика,
автор: ainuraaa17
Помогите предел решить пожалуйста
Приложения:
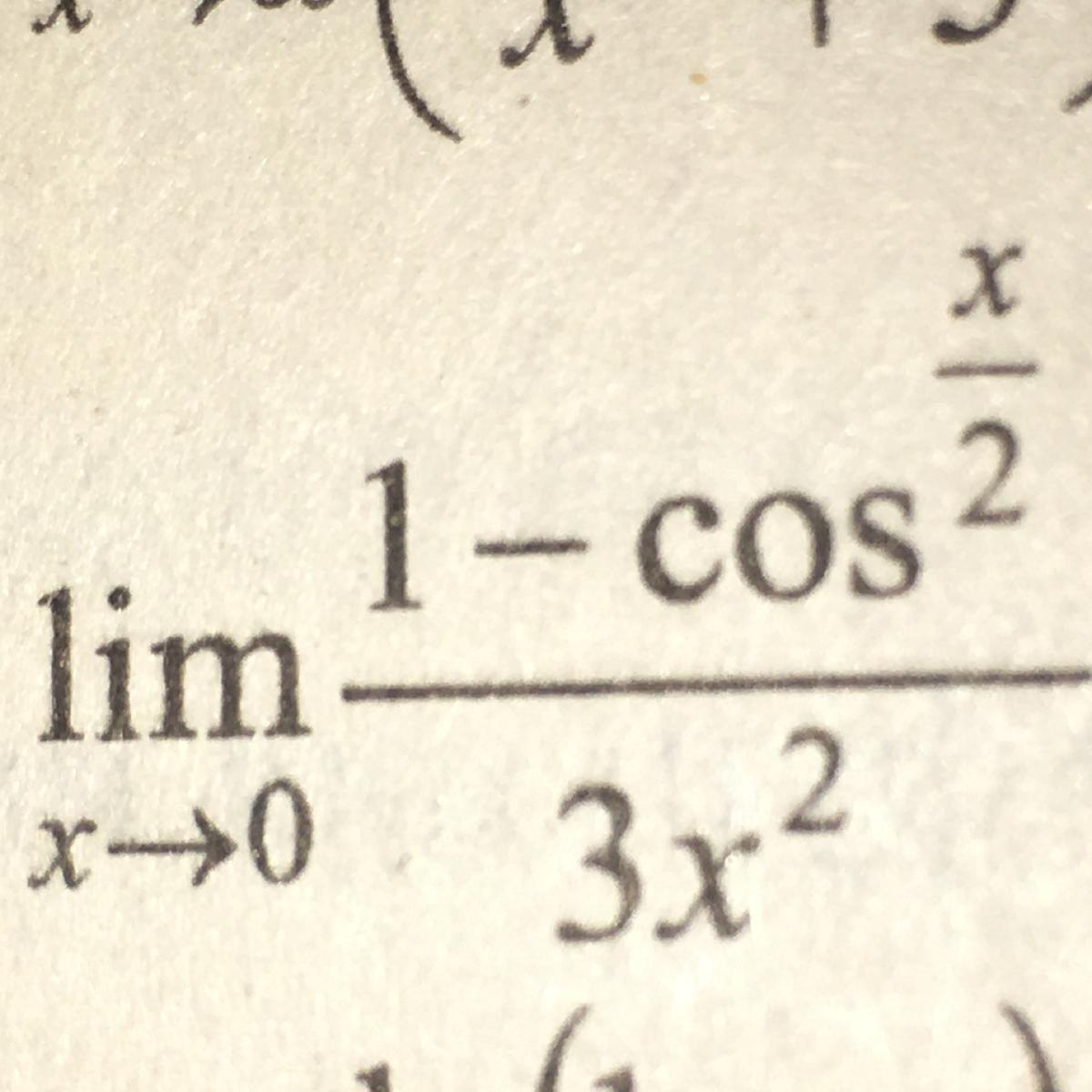
Ответы
Автор ответа:
1
Ответ:
на фотографии
Пошаговое объяснение: для cosx при икс, устремленном к нулю, эквивалент бесконечно малой величины составляет: cosx ≅
для соответственно:
≅
Приложения:


ainuraaa17:
Пжжж
значит x/2 - это не степень, а аргумент косинуса, как на снимке. Тригонометрическая функция не имеет смысла без аргумента, от которого она берется
не может косинус или синус возводиться в какую-то степень, не имея при себе аргумента или угла
в общем, пусть модератор определит: верно решение или нет
Действительно , с ответами сверила , правильно
Спасибо
Только мы через производную не пишем
можно и через ряд Тейлора выполнить
Выполнишь?)))
Пжжж
Похожие вопросы
Предмет: Окружающий мир,
автор: мишатиша
Предмет: Русский язык,
автор: samir1812
Предмет: Русский язык,
автор: саша200702саша
Предмет: Физика,
автор: AnNoChKaloving
Предмет: География,
автор: Еміліана1