Question

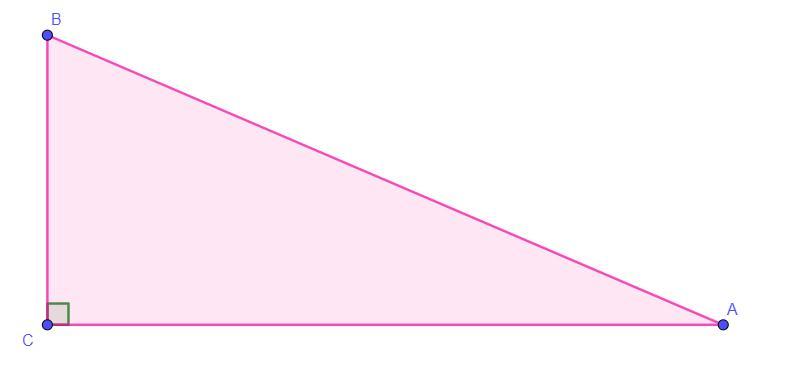
Дан треугольник ABC, в котором ∠C=90°, а sinB = (4√3):(10√5). Найди cos в квадрате B.

Answer 1

Ответ:

$\boxed{\ cos^{2} \angle B = \dfrac{113}{125}}$

Объяснение:

Так как угол ∠B является углом прямоугольного треугольника, то $\cos \angle B > 0$. По основному тригонометрическому тождеству:

$\sin^{2} \angle B + \cos^{2} \angle B = 1$

$\cos^{2} \angle B = 1 - \sin^{2} \angle B = 1 - (\frac{4\sqrt{3} }{10\sqrt{5} })^{2} = 1 - \dfrac{16 * 3}{100 * 5} = 1 - \dfrac{12}{125} = \dfrac{125 - 12}{125}=$

$= \dfrac{113}{125}$.