Предмет: Математика,
автор: bahytzankyzyalbina
Помогите пожалуйста
Приложения:
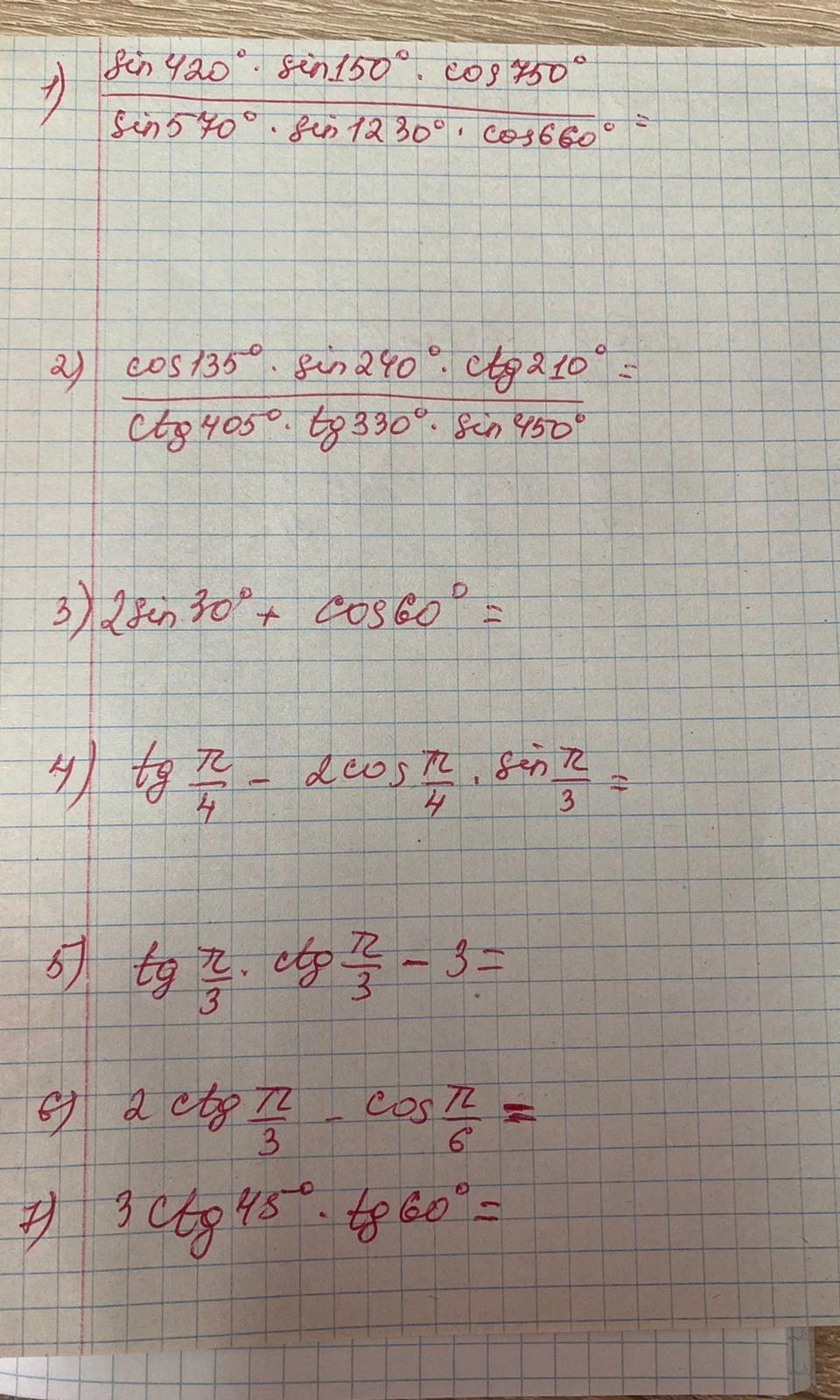
Ответы
Автор ответа:
1
Теория
если:
если:
1) Вычислим значения функций и перепишем выражение
2)
3)
4)
5)
6)
7)
Похожие вопросы
Предмет: Английский язык,
автор: kdaniil05
Предмет: Українська мова,
автор: natasha1982n
Предмет: Русский язык,
автор: руфат5
Предмет: Русский язык,
автор: Mallka12309
Предмет: Математика,
автор: Nikblack9131