Предмет: Алгебра,
автор: Аноним
Помогите с примером на доказательство (Комплексные числа)
Приложения:
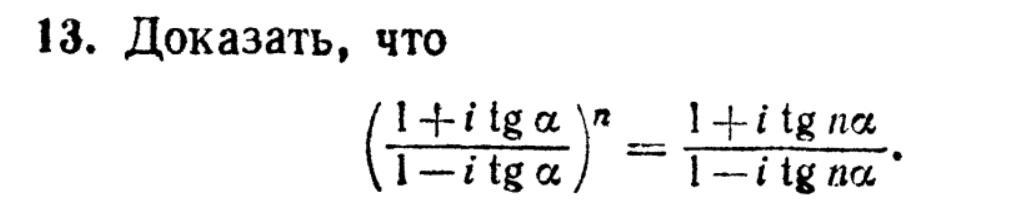
Ответы
Автор ответа:
1
Ч.т.д.
Похожие вопросы
Предмет: Русский язык,
автор: elgunp
Предмет: Английский язык,
автор: kitty33
Предмет: Английский язык,
автор: zenbzirou
Предмет: Геометрия,
автор: Ogyrecik007
Предмет: Русский язык,
автор: ItsNoymi