Предмет: Алгебра,
автор: Аноним
Помогите с примером(Комплексные числа)
Приложения:
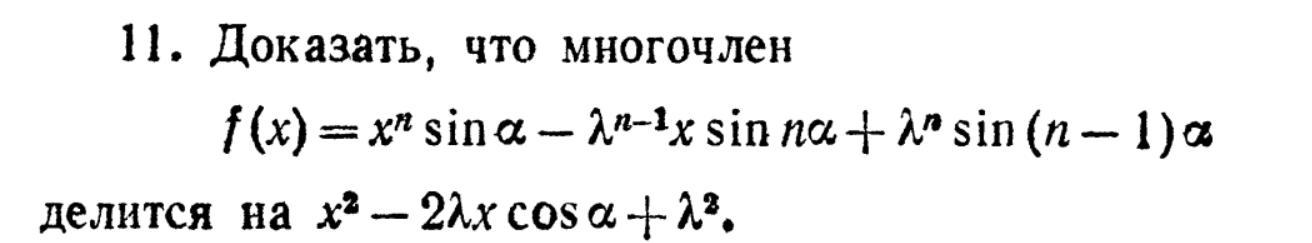
Ответы
Автор ответа:
2
Но тогда
1)
,
Т.е. является нулем многочлена
.
2)
Т.е. является нулем многочлена
.
Но это и означает делимость многочлена на произведение
, т.е. на
Ч.т.д.
Похожие вопросы
Предмет: Английский язык,
автор: zenbzirou
Предмет: Английский язык,
автор: rebrova08
Предмет: Русский язык,
автор: girlfantastic
Предмет: Математика,
автор: Крисмик
Предмет: Биология,
автор: kaspa02