Предмет: Алгебра,
автор: ShmigaRoblox
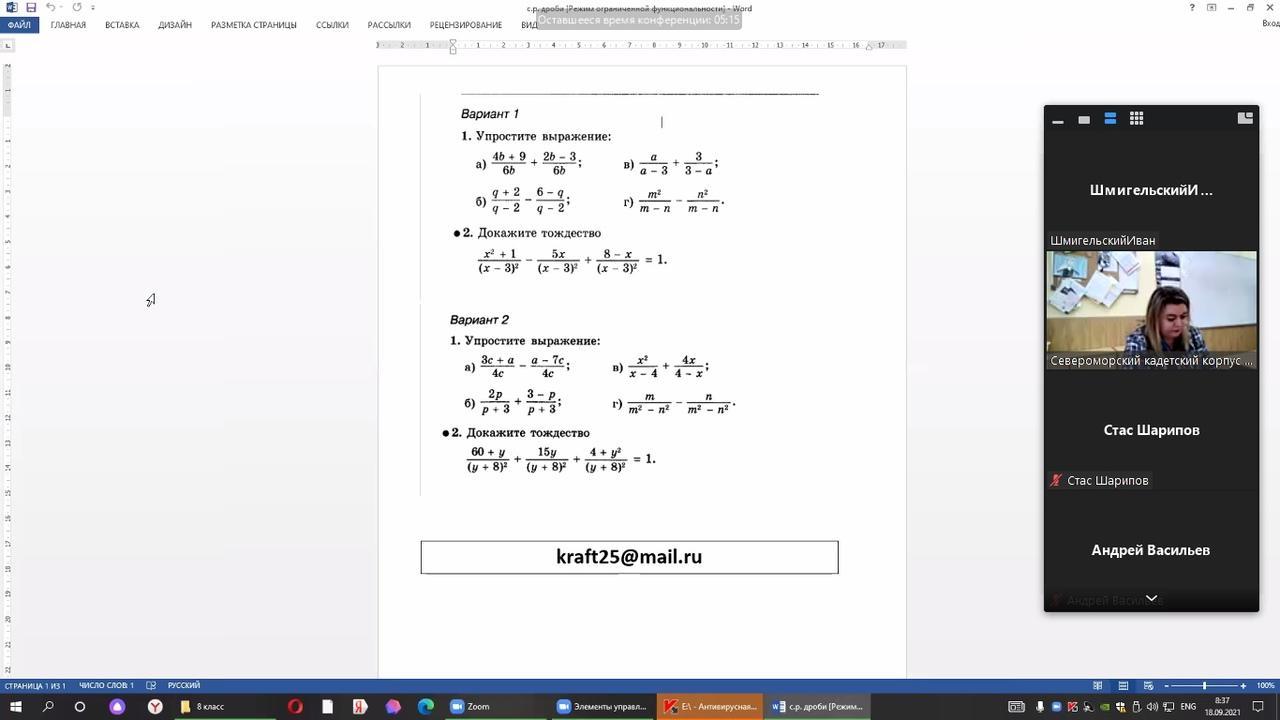
Помогите решить пожалуйста алгебру, задание на время!!!!!!!!!!!!!
Приложения:
ShmigaRoblox:
мне только 1 вариант надо
Ответы
Автор ответа:
1
1 вариант.
1.
а)
б)
в)
г)
2.
2 вариант.
1.
а)
б)
в)
г)
2.
Похожие вопросы
Предмет: Английский язык,
автор: kitty33
Предмет: Другие предметы,
автор: lpfmms1
Предмет: Українська мова,
автор: дашаку
Предмет: Физика,
автор: alexsandra2515
Предмет: Химия,
автор: SweetCandy23228