Предмет: Алгебра,
автор: user05li
Помогите пожалуйста
Приложения:
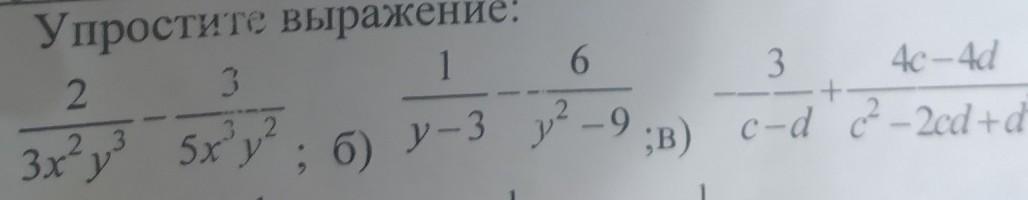
Ответы
Автор ответа:
1
Объяснение:
А.
Б.
В.
Автор ответа:
1
Объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: andjylika
Предмет: Английский язык,
автор: igdarya
Предмет: Другие предметы,
автор: всемпофиг
Предмет: Русский язык,
автор: MilaAlexMigel