Предмет: Алгебра,
автор: Cef1rka
найти первообразную функции а) г)
Приложения:
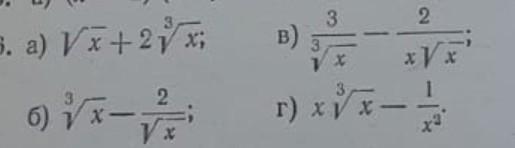
Ответы
Автор ответа:
0
Объяснение:
a)
г)
Похожие вопросы
Предмет: Английский язык,
автор: yfqkz
Предмет: Окружающий мир,
автор: анастасия761
Предмет: Русский язык,
автор: den863989737
Предмет: Математика,
автор: fmjhgf
Предмет: Русский язык,
автор: чекпо