Предмет: Геометрия,
автор: klopvanuchka
СРОЧНО ПОМОГИТЕ РЕШИТЬ ЗАДАЧУ, ПОЖАЛУЙСТА!
Приложения:
Аноним:
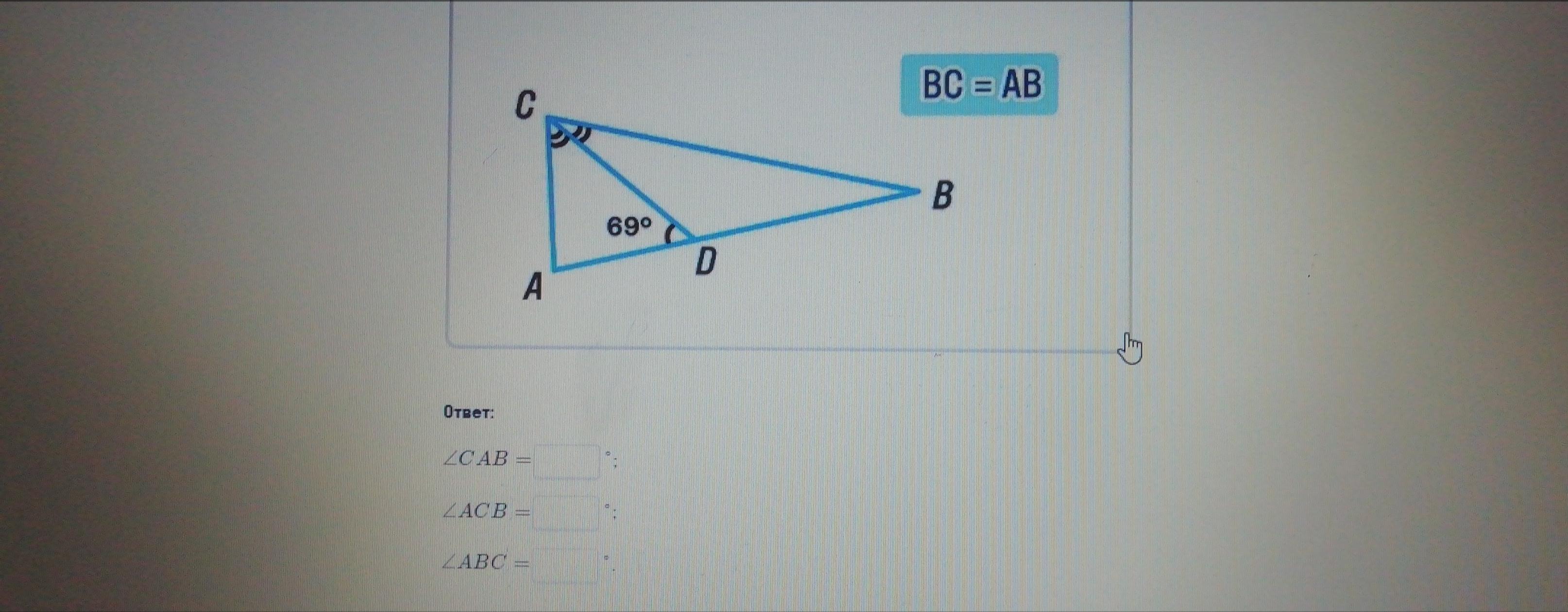
САВ=74
АСВ=74
АВС=32
Ответы
Автор ответа:
0
Ответ:
< CAB = 74°,
< ACB = 74°,
< ABC = 32°
Объяснение:
B = BC => ∆ABC — равнобедренный, значит
<А = <С
<АСD = <BCD = 1/2 <C
Рассмотрим ∆АСD
Возьмем угол А за x, угол АСD за x/2.
Сумма углов треугольника равна 180°
Угол А равен 74°, тогда <ACD равен
Угол ACB (<C) = <А = 74°
Угол ABC (<B) равен:
Похожие вопросы
Предмет: Русский язык,
автор: анна661
Предмет: Другие предметы,
автор: дианаагасян
Предмет: Другие предметы,
автор: всемпофиг
Предмет: Математика,
автор: хелп46