Question

Пожалуйста решите с рисунком, (сам хочу понять как правильно решать).
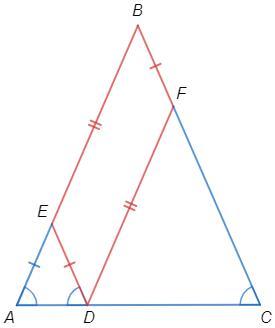
На основании равнобедренного треугольника взята произвольная точка и через неё проведены две прямые, параллельные боковым сторонам. Периметр полученного параллелограмма равен 24 см . Найдите боковую сторону треугольника.

Answer 1

Ответ:

AB=12 см

Объяснение:

△ABC -р/б => ∠A=∠C (углы при основании)

DE||BC => ∠EDA=∠C (соответственные углы)

=> ∠EDA=∠A => △AED -р/б (по признаку), AE=DE

P(DEBF) =2(DE+EB) =24

=> DE+EB=12 => AE+EB=12 =AB